Linear Approximation and Differential of a function of several variables

Linear Approximation and Differential of a function of several variables

Earlier in this chapter, we have seen that linear approximation and differential of a function of one variable. Here we introduce similar ideas for functions of two variables and three variables. In general for functions of several variables these concepts can be defined similarly.

Definition 8.10

Let A = {( x, y ) | a < x < b, c < y < d } ⊂ ℝ² , F : A → ℝ, and ( x₀ , y₀ ) ∈ A .

(i) The linear approximation of F at ( x₀ , y₀ ) ∈ A is defined to be

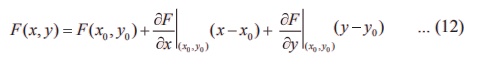
(ii) The differential of F is defined to be

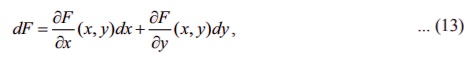
where dx = Δx and dy = Δy,

Here we shall outline the linear approximations and differential for the functions of three variables. Actually, we can define linear approximations and differential for real valued function having more variables, but we restrict ourselves to only three variables.

Definition 8.11

Let A = {( x, y , z) | a < x < b, c < y < d, e < z < f } ⊂ ℝ³, F : A → ℝ and ( x₀ , y₀ , z₀ ) ∈ A .

(i) The linear approximation of F at ( x₀ , y₀ , z₀ ) ∈ A is defined to be

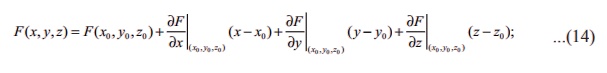
(ii) The differential of F is defined by

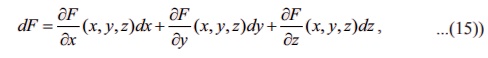
where dx = Δx , dy = Δy and dz = Δz ,

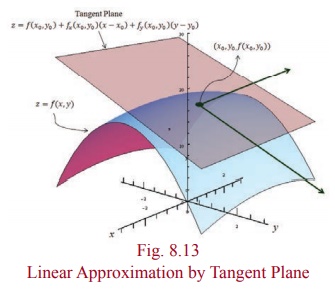
Geometrically, in the case of function f of one variable, the linear approximation at a point x₀ represents the tangent line to the graph of y = f ( x) at x₀ . Similarly, in the case of a function F of two variables, the linear approximation at a point ( x₀ , y₀ ) represents the tangent plane to the graph of z = F ( x , y) at ( x₀ , y₀ ) .

Example 8.16

If w( x, y , z) = x²y + y²z + z²x, x , y, z ∈ ℝ, find the differential dw.

Solution

First let us find w_x , w_y , and w_z .

Now w_x = 2xy + z², w_y = 2yz + x² and w_Z = 2zx + y².

Thus,by (15), the differential is

dw = (2xy + z² )dx + (2 yz + x² )dy + (2zx + y²)dz .

Example 8.17

Let U ( x, y , z) = x ² − xy + 3sin z, x , y, z ∈ ℝ. Find the linear approximation for U at (2, −1, 0) .

Solution

By (14), linear approximation is given by

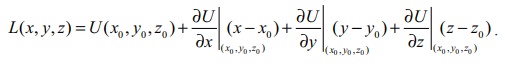
Now U_x = 2x − y , U_y = − x and U _z = 3cos z .

Here (x₀ , y₀ , z₀ ) = (2, −1, 0) , hence U_x (2, −1, 0) = 5, U_y (2, −1, 0) = −2 and U_z (2, −1, 0) = 3 .

Thus L ( x, y , z) = 6 + 5(x − 2) − 2( y + 1) + 3(z − 0) = 5x − 2 y + 3z − 6 is the required

Linear approximation for U at (2, −1, 0) .