Functions of Several Variables

Functions of Several Variables

Recall that given a function f of x ; we sketch the graph of y = f ( x) to understand it better. Generally, the graph of y = f ( x) gives a curve in the xy -plane. Also, the derivative f ′(a) of f at x = a represents the slope of the tangent at x = a , to the graph of f . In the introduction we have seen the need for considering functions of more than one variable. Here we shall develop some concepts to understand functions of more than one variable. First we shall consider functions of two variables. Let F ( x, y) be a function of x and y . To obtain graph F , we graph z = F ( x , y) in the xyz -space. Also, we shall develop the concepts of continuity, partial derivatives of a function of two variables.

Let us look at an example, g ( x, y ) = 30 − x² − y² , for x , y ∈ ℝ. Given a point ( x , y) ∈ ℝ², then z = 30 − x² − y² gives the z coordinate of the point on the graph. Thus the point (x , y, 30 − x² − y² ) lies 30 − x² − y² high just above the point ( x , y) in xy -plane. For instance, for (2, 3) ∈ ℝ² , the point (2, 3, 30 − 2² − 3² ) = (2, 3,17) lies on the graph of g . If we fix the value y = 3 , then g ( x, 3) = −x² + 21 which is a function that depends only on x variable; so its graph must be a curve. Similarly, if we fix value x = 2 , then we have g (2, y) = 26 − y² which is a function that depends only on y . In each case the graph, as the resulting function being quadratic, will be a parabola. The surface we obtain from z = g( x , y) is called paraboloid.

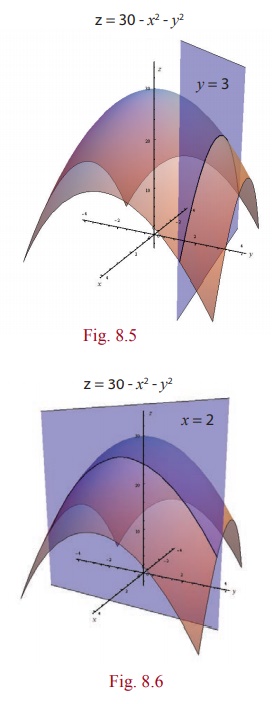
Note that g ( x, 3) = 21− x² represents a parabola; which is obtained by intersecting the surface of z = 30 − x² − y² with the plane y = 3 [see Fig. 8.5). Similarly g (2, y) = 26 − y² represents a parabola; which is obtained by intersecting the surface of z = 30 − x² − y² with the plane x = 2 [see Fig. 8.6). Following graphs describes the above discussion.

z = 30 - x² - y^{2 ,} z = 30 - x² - y²

In the same way, given a function F of a two variables say x , y , we can visualize it in the three space by considering the equation z = F ( x , y) . Generally, this will represent a surface in ℝ³.