Mathematics - Limit and Continuity of Functions of Two Variables | 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Chapter: 12th Maths : UNIT 8 : Differentials and Partial Derivatives
Limit and Continuity of Functions of Two Variables
Limit and
Continuity of Functions of Two Variables
Definition 8.6 (Limit of a Function)
Suppose that A {( x ,
y) | a < x < b , c < y < d
} ŌŖé ŌäØ2 , F : A ŌåÆ R. We say
that F has a limit L at (u,v) if the
following hold :
For every neighboourhood ( L ŌłÆ ╬Ą , L + ╬Ą ), ╬Ą > 0 , of L , there
exists a ╬┤ ŌĆōneighbourhood B╬┤ ((u,
v )) ŌŖé A of (u,v) such that
( x , y) Ōłł B╬┤ ((u, v ))
\ {(u, v )}, ╬┤ > 0 ŌćÆ f (x) Ōłł(L ŌłÆ ╬Ą , L + ╬Ą ) .
We denote this by lim (
x , y ) ŌåÆ(u,v) F ( x, y ) = L
if such a limit exists.
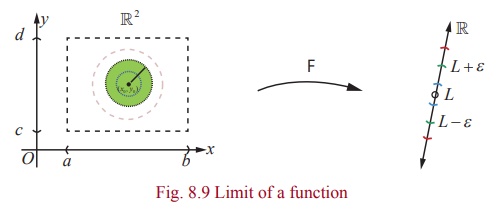
When
compared to the case of a function of single variable, for a function of two
variables, there is a subtle depth in the limiting process. Here the values of F ( x,
y) should approach the same value L , as ( x , y) approaches (u , v)
along every
possible path to (u , v) (including paths that are not
straight lines). Fig.8.9 explains the limiting process.
All the rules for
limits (limit theorems) for functions of one variable also hold true for
functions of several variables.
Now,
following the idea of continuity for functions of one variable, we define
continuity of a function of two variables.
Definition 8.7 (Continuity)
Suppose that A = {( x, y ) | a < x < b, c < y < d } ŌŖé ŌäØ2 , F : A ŌåÆ ŌäØ. We say that F is
continuous at at (u , v) if the following hold :
(1) F is defined at (u , v)
(2) lim( x , y ) ŌåÆ(u,v) F ( x, y ) = L
exists
(3) L = F (u,v).
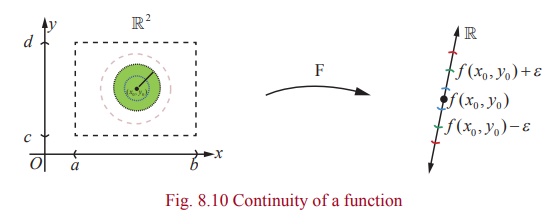
Remark
(1) In
Fig. 8.10 taking L =
F ( x0 , y0
) will illustrate continuity at ( x0
, y0 ) .
(2) Continuity
for f (x1 , x2
, , xn ) is also defined
similarly as defined above.
Let us
consider few examples as illustrations to understand continuity of functions of
two variables.
Example 8.8
Let f (x
, y) =  (or) 3xŌłÆ5y+8 / x2+y2+1
for all ( x , y) Ōłł ŌäØ2. Show that f is continuous on ŌäØ2.
(or) 3xŌłÆ5y+8 / x2+y2+1
for all ( x , y) Ōłł ŌäØ2. Show that f is continuous on ŌäØ2.
Solution
Let (a ,
b) Ōłł ŌäØ2 be an arbitrary point. We shall
investigate continuity of f at (a ,
b).
That is,
we shall check if all the three conditions for continuity hold for f at (a , b) .
To check
first condition, note that f (a, b) =  is defined.
is defined.
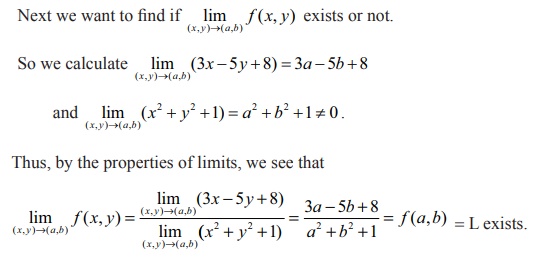
Now we
note that limx,yŌåÆ( a , b) f (x, y ) = L = f (a, b) . Hence f satisfies all the three conditions for continuity of f at (a , b) . Since (a , b) is an
arbitrary point in ŌäØ2 , we conclude that f is continuous at every point of ŌäØ2.
Example 8.9
Consider
f ( x, y) = 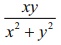 if (
x , y) ŌēĀ (0, 0) and f (0, 0) = 0
. Show that f is not continuous
at (0, 0) and continuous at all other points of ŌäØ2 .
if (
x , y) ŌēĀ (0, 0) and f (0, 0) = 0
. Show that f is not continuous
at (0, 0) and continuous at all other points of ŌäØ2 .
Solution
Note
that f is defined for every ( x , y)
Ōłł R2 . First let us check the continuity at ( a , b)
ŌēĀ
(0, 0) .
Let us
say, just for instance, (a , b) = (2, 5) . Then f (2, 5) = 10/29 . Then, as in the above
example, we calculate
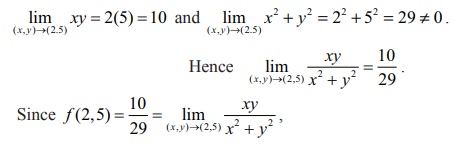
it follows that f is continuous at (2, 5) .
Exactly by
similar arguments we can show that f is
continuous at every point ( a , b) ŌēĀ
(0, 0) . Now let us check the continuity at (0, 0) . Note that f (0, 0) = 0 by definition. Next we want
to find if
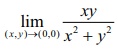
exists
or not.
First
let us check the limit along the straight lines y = mx , passing through
(0, 0).
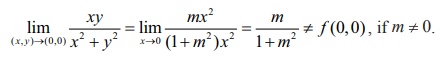
So for
different values of m , we get
different values m / 1+ m2 and
hence we conclude that 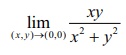 does not exist. Hence f cannot be continuous at (0, 0) .
does not exist. Hence f cannot be continuous at (0, 0) .
Example 8.10
Consider g ( x
, y) = 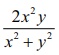 if ( x , y) ŌēĀ
(0, 0) and g(0, 0) = 0. Show that g is
continuous on ŌäØ2.
if ( x , y) ŌēĀ
(0, 0) and g(0, 0) = 0. Show that g is
continuous on ŌäØ2.
Solution
Observe
that the function g is defined for
all ( x , y) Ōłł
ŌäØ2 . It is easy to check, as in the
above examples, that g is continuous
at all point ( x , y) ŌēĀ (0, 0) . Next we shall check the
continuity of g at (0, 0) . For that
we see if g has a limit L at (0, 0) and if L = g(0, 0) =
0 . So we consider
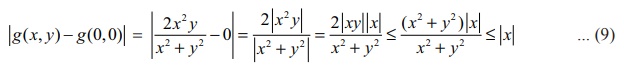
Note
that in the final step above we have used 2|xy|
Ōēż x2 + y2 (which
follows by considering 0 Ōēż (x ŌłÆ y)2 )
for all x , y Ōłł ŌäØ. Note that ( x , y) ŌåÆ
(0, 0) implies |x| ŌåÆ
0 . Then from (9) it follows that 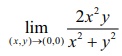 = 0 = g(0, 0) ; which proves that g is continuous at (0, 0) . So g is continuous at every point of ŌäØ2.
= 0 = g(0, 0) ; which proves that g is continuous at (0, 0) . So g is continuous at every point of ŌäØ2.
Related Topics