Chapter: 11th Chemistry : UNIT 9 : Solutions
Solved Example Problems: Chemistry: Solutions
Chemistry: Solutions
Numerical Problems Questions with Answers, Solution
Example Problem 1
1. What volume of 4M HCl and 2M HCl should be mixed to get 500 mL of 2.5 M HCl?
Let the volume of 4M HCl required to prepare 500 mL of 2.5 MHCl = x mL
Therefore, the required volume of 2M HCl = (500 - x) mL
We know from the equation (9.1)
C1V1+ C2V2 = C3V3
(4x)+2(500-x) = 2.5 × 500
4x+1000-2x = 1250
2x = 1250 - 1000
x = 250/2
= 125 mL
Hence, volume of 4M HCl required = 125 mL
Volume of 2M HCl required = (500 - 125) mL= 375 mL
Example Problem 2:
0.24 g of a gas dissolves in 1 L of water at 1.5 atm pressure. Calculate the amount of dissolved gas when the pressure is raised to 6.0 atm at constant temperature.
psolute = KHxsolute in solution
At pressure 1.5 atm,
p1 = KH x1------------(1)
At pressure 6.0 atm,
p2 = KH x2------------(2)
Dividing equation (1) by (2)
From equation p1/p2 = x1/x2
1.5/6.0 = 0.24/x2
Therefore x2 = 0.24 x 6.0/1.5 = 0.96 g/L
Example Problem 3:
An aqueous solution of 2 % nonvolatile solute exerts a pressure of 1.004 bar at the boiling point of the solvent. What is the molar mass of the solute when PA° is 1.013 bar?
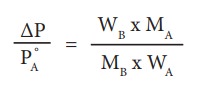
In a 2 % solution weight of the solute is 2 g and solvent is 98 g
ΔP = PA° – Psolution= 1.013 -1.004 bar = 0.009 bar
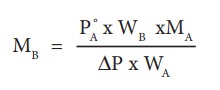
MB = 2 x 18 x 1.013/(98 x 0.009)
= 41.3 g mol-1
Example Problem 4
0.75 g of an unknown substance is dissolved in 200 g water. If the elevation of boiling point is 0.15 K and molal elevation constant is 7.5 K Kg mol-1 then, calculate the molar mass of unknown substance
ΔTb = Kb m
= Kb x W2 x 1000 / M2 x W1
M2 = Kb x W2 x 1000 / ΔTb x W1
= 7.5 x 0.75 x 1000 / 0.15 x 200
= 187.5 g mol-1
Example Problem 5
Ethylene glycol (C2H6O2) can be at used as an antifreeze in the radiator of a car. Calculate the temperature when ice will begin to separate from a mixture with 20 mass percent of glycol in water used in the car radiator. Kf for water = 1.86 K Kg mol-1 and molar mass of ethylene glycol is 62 g mol-1.
Weight of solute (W2) = 20 mass percent of solution means 20 g of ethylene glycol
Weight of solvent (water) W1 = 100 -20 = 80 g
ΔTf = Kfm
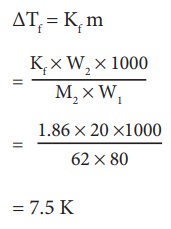
= 7.5 K
The temperature at which the ice will begin to separate is the freezing of water after the addition of solute i.e 7.5 K lower than the normal freezing point of water (273-7.5K) = 265.5 K
Example Problem-6 :
At 400K 1.5 g of an unknown substance is dissolved in solvent and the solution is made to 1.5 L. Its osmotic pressure is found to be 0.3 bar. Calculate the molar mass of the unknown substance.
Example Problem – 7
The depression in freezing point is 0.24K obtained by dissolving 1g NaCl in 200g water. Calculate van’t-Hoff factor. The molal depression constant is 1.86 K Kg mol-1
Molar mass of solute
40. A sample of 12 M Concentrated hydrochloric acid has a density 1.2 gL–1 Calculate the molality
Solution:
Molality = 12 M HCl
density of the solution = 1.2 gL−1
In 12 M HCl solution, there are 12 moles of HCl in 1 litre of the solution
Molality = no. of moles of solute / mass of solvent (in Kg)
Calculate mass of water (solvent) mass of 1 litre HCl solution = density × volume
= 1.2 gmL−1 × 1000 ml = 1200 g
mass of HCl = no. of moles of HCl × molar mass of HCl
= 12 mol × 36.5 g mol−1 = 438 g
mass of water = mass of HCl solution − mass of HCl
mass of water = 1200 − 438 = 762 g
molality = 12 / 0.762
= 15.75 m
41. A 0.25 M glucose solution at 370.28 K has approximately the pressure as blood does what is the osmotic pressure of blood ?
Solution:
C = 0.25m
T= 370.28 K
(π)glucose = CRT
(π) = 0.25molL−1 × 0.082L atm K−1 mol−1 × 370.28K
= 7.59 atm
42. Calculate the molality of a solution containing 7.5 g of glycine (NH2-CH2 -COOH) dissolved in 500 g of water.
Solution:
molality = no. of moles of solute / mass of solvent (in Kg)
no. of moles of glycine = mass of glycine / molar mass of glycine = 7.5 / 75 = 0.1
molality = 0.1 / 0.5 Kg = 0.2 m
43. Which solution has the lower freening point?10 g of methanol (CH3OH) in 100g of water (or) 20 g of ethanol (C2H5OH) in 200 g of water.
Solution:
ΔTf = Kf m ; ie ΔTf ∝ m
m(CH3OH) = (10/32) / 0.1 = 3.125m
M(C2H5OH) = (20/46) / 0.2 = 2.174m
∴ depression in freezing point is more in methanol solution and it will have lower freezing point.
44. How many moles of solute particles are present in one litre of 10-4 M potassium sulphate?
Solution:
In 10-4 M K2SO4 solution, there are 10-4 moles of potassium sulphate.
K2SO4 molecule contains 3 ions (2K+ and 1 SO42− )
1 mole of K2SO4 contains 3 × 6.023×1023 ions
10-4 mole of K2SO4 contains 3 × 6.023×1023 × 10−4 ions
= 18.069×1019
45. Henry’s law constant for solubility of methane in benzene is 4.2x10-5 mm Hg at a particular constant temperature At this temperature. Calculate the solubility of methane at i) 750 mm Hg ii) 840 mm Hg
Solution:
(kH )benzene = 4.2 × 10-5 mm Hg ;
Solubility of methane = ?
P = 750mm Hg
P = 840 mm Hg
According to Henry's Law
P = KH.x in solution
750mm Hg = 4.2 x 10-5 mm Hg.xin solution
⇒ xin solution = 750 / (4.2×10-5)
i.e. solubility, = 178.5 × 105 = 1.785 × 105
similarly at P = 840 mm Hg
solubility = 840 / 4.2×10-5
= 200 × 10-5
46. The observed depression in freezing point of water for a particular solution is 0.093ºC. Calculate the concentration of the solution in molality. Given that molal depression constant for water is 1.86 KKg mol-1
Solution:
ΔTf = 0.093°C = 0.093K ;
m = ?
Kf = 1.86 K Kg mol−1 ;
ΔTf = Kf.m
∴ μ = ΔTf / Kf
m = 0.093K / 1.86 K Kg mol−1
= 0.05 mol Kg −1 = 0.05 m.
47. The vapour pressure of pure benzene (C6H6) at a given temperature is 640 mm Hg. 2.2 g of non-volatile solute is added to 40 g of benzene. The vapour pressure of the solution is 600 mm Hg. Calculate the molar mass of the solute?
Solution:
P°C6H6 = 640 mm Hg
W2 = 2.2 g (non volatile solute)
W1 = 40 g (benzene)
Psolution = 600mm Hg
M2 = ?
(P°−P) / P° = X2 ;
(640 – 600) / 640 = n2 / n1 + n2 [∵ n1 >> n2 ; n1 + n2 = n1 ]
40 / 640 = n2 / n1
0.0625 = ( W2 × M1 ) / (M2 × W1)
M2 = (2.2 × 78) / (0.0625 × 40) = 68.64 g mol−1
Related Topics