Abnormal molar mass

Abnormal molar mass

The molar masses of the nonvolatile solutes can be calculated accurately using the experimentally determined colligative properties. In this method, we assume that the solution is very dilute and there is no dissociation or association of solute particles in the solution.

In a concentrated solution, the interaction between the solute and solvent becomes significant and reflected in the measured colligative properties. Similarly, the dissociation or association of solute molecules would alter the total number of particles present in the solution and hence affect the results of measured colligative properties. In such solutions, the value of the molar mass of the solute determined using colligative properties would be different from the actual molar mass, and it is called abnormal molar mass.

Association or dissociation of solute molecules:

Normally, the molar mass determination using measured colligative properties assumes that the solute does not dissociate or associate. In certain solvents, solute molecules associate to form a dimer or trimer etc… This reduces the total number of particles (molecules) formed in solution and as a result the calculated molar mass will be higher than the actual molar mass. Let us consider a solution of acetic acid in benzene. It is already established that acetic acid forms inter molecular hydrogen bonds as shown in the figure 9.9 and exists as a dimer in benzene.

2CH₃COOH →(CH₃COOH)₂

The molar mass of acetic acid calculated using colligative properties is found to be around 120 g mol-1 is two times the actual molar mass (60 g mol^-1).

The electrolytes such as KCl or NaCl dissociates completely into its constitutent ions in their aqueous solution. This causes an increase in the total number of particles (ions) present in the solution. The calculated molar mass using colligative property measurement for this type of solutions will be lower than the actual molar mass. For example, the sodium chloride dissociates into Na+ ions and Cl- ions in aqueous solution, as shown below.

NaCl (s) → Na⁺ (aq) + Cl^– (aq)

When we dissolve 1 mole of NaCl (58.4 g) in water, it dissociates and gives 1 mole of Na⁺ and 1 mole of Cl^-. Hence, the solution will have 2 moles of particles. Thus, the colligative properties would be double the expected value.

van’t Hoff factor

We have learnt that the dissociation or association of solute molecules in a solution will result in the increase or decrease in the calculated molar mass using the colligative property. This variation is proportional to the extent of association or dissociation. To quantify the extent of association or dissociation of solutes in solution, van’t Hoff introduced a term 'i' which is now called van’t Hoff factor. It is defined as the ratio of the actual molar mass to the abnormal (calculated) molar mass of the solute. Here, the abnormal molar mass is the molar mass calculated using the experimentally determined colligative property.

i = Normal (actual) molar mass / Observed (abnormal) molar mass

= Observed colligative property / Calculated colligative property

The estimated Van’t Hoff factor for acetic acid solution in Benzene is 0.5 and that of sodium chloride solution in water is 2. The degree of dissociation or association can be related to Van't Hoff factor (i) using the following relationships

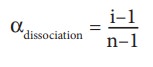
(Where n is number ions /species formed by the dissociation of a single molecule)

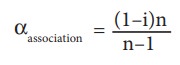
(here, n is the number of solute involved in association.

The equations relating the four colligative properties with the concentration of the solutes can be rewritten as follow by incorporating the van’t Hoff factor

Relative lowering of vapour pressure,

Elevation of boiling point

∆T_b =iK_bm

Depression in the freezing point

∆T_f  = iK_f m

Osmotic pressure

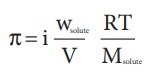
For a solute that does not dissociate or associate the van’t Hoff factor is equal to 1 (i = 1) and the molar mass will be close to the actual molar mass.

For the solutes that associate to form higher oligomers in solution the van’t Hoff factor will be less than one (i <1) and the observed molar mass will be greater than the actual molar mass.

For solutes that dissociates into their constituent ions the van’t Hoff factor will be more than one (i > 1) and the observed molar mass will be less than the normal molar mass.

Example Problem – 7

The depression in freezing point is 0.24K obtained by dissolving 1g NaCl in 200g water. Calculate van’t-Hoff factor. The molal depression constant is 1.86 K Kg mol^-1

Molar mass of solute