Vapour pressure of liquid solutions

Vapour pressure of liquid solutions

When a solute (of any physical state - solid, liquid or gas ) is dissolved in a liquid solvent the resultant solution is called a liquid solution. The solution which contains only two components (one solvent and one solute) is called a binary solution. We have already discussed the solution of a gaseous solute in liquid solvent under Henry's law.

Vapour pressure of binary solution of liquid in liquids

Now, let us consider a binary liquid solution formed by dissolving a liquid solute ‘A’ in a pure solvent ‘B’ in a closed vessel. Both the components A and B present in the solution would evaporate and an equilibrium will be established between the liquid and vapour phases of the components A and B.

The French chemist Raoult, proposed a quantitative relationship between the partial pressures and the mole fractions of two components A & B, which is known as Raoult’s Law. This law states that “in the case of a solution of volatile liquids, the partial vapour pressure of each component (A & B) of the solution is directly proportional to its mole fraction”.

According to Raoult’s law,

p_Aα x_A (9.3)

p_A = k x_A

when x_A = 1, k = p°_A

where p°_A is the vapour pressure of pure component ‘A’ at the same temperature.

Therefore,

p_A = p°_AX_A  (9.4)

Similarly, for component ‘B’

p_B= p°_B x_B    (9.5)

x_A and x_B are the mole fraction of the components A and B respectively.

According to Dalton’s law of partial pressure the total pressure in a closed vessel will be equal to the sum of the partial pressures of the individual components.

Hence,

P_total = p_A + p_B (9.6)

Substituting the values of p_A and p_B from equations (9.4) and (9.5) in the above equation,

P_total = x_Ap°_A + x_Bp°_B (9.7)

We know that x_A + x_B = 1 or x_A = 1 - x_B

Therefore,

P_total = (1 - x_B) p°_A + x_B p°_B (9.8)

P_total= p°_A + x_B( p°_B- p°_A) (9.9)

The above equation is of the straight-line equation form y = mx+c. The plot of P_total versus x_a will give a straight line with (p_B°- p_A°) as slope and p_A° as the y intercept.

Let us consider the liquid solution containing toluene (solute) in benzene (solvent).

The variation of vapour pressure of pure benzene and toluene with its mole fraction is given in the graph.

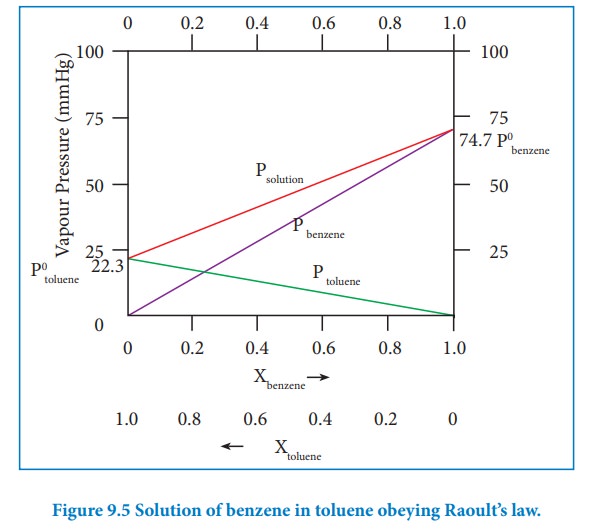
The vapour pressures of pure toluene and pure benzene are 22.3 and 74.7 mmHg, respectively. The above graph shows, the partial vapour pressure of the pure components increases linearly with the increase in the mole fraction of the respective components. The total pressure at any composition of the solute and solvent is given by the following straight line (represented as red line) equation.

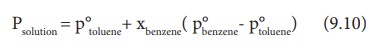
Vapour pressure of binary solution of solids in liquids

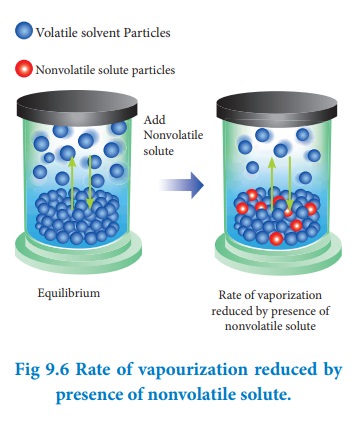
When a nonvolatile solute is dissolved in a pure solvent, the vapour pressure of the pure solvent will decrease. In such solutions, the vapour pressure of the solution will depend only on the solvent molecules as the solute is nonvolatile.

For example, when sodium chloride is added to the water, the vapour pressure of the salt solution is lowered. The vapour pressure of the solution is determined by the number of molecules of the solvent present in the surface at any time and is proportional to the mole fraction of the solvent.

P_solution ∝x_A (9.11)

Where x_A is the mole fraction of the solvent

P_solution    =   k x_A  (9.12)

When x_A  = 1,    K   = P^o_solvent

(P_solvent^o is the partial pressure of pure solvent)

P_solution    =   P^o_solvent x_A  (9.13)

Where x_B is the fraction of the solute

(_∴ x_{A +} x_B = 1, x_B = 1 - x_A)

The above expression gives the relative lowering of vapour pressure. Based on this expression, Raoult’s Law can also be stated as “the relative lowering of vapour pressure of an ideal solution containing the nonvolatile solute is equal to the mole fraction of the solute at a given temperature”.

Comparison of Raoult’s law and Henry’s law

According to Raoult’s law, for a solution containing a nonvolatile solute

p_solute = p°_solutex_solute (9.17)

According to Henry’s law:

p_solute = K_Hx_{solute in solution} (9.18)

The difference between the above two expressions is the proportionality constant p°_A (Raoults Law) and K_H .(Henry's Law). Henry's law is applicable to solution containing gaseous solute in liquid solvent, while the Raoults Law is applicable to nonvolatile solid solute in a liquid solvent. If the solute is non volatile then the Henry's law constant will become equal to the vapour of the pure solvent (p°) and thus, Raoult’s law becomes a special ^Acase of Henry’s law. For very dilute solutions the solvent obeys Raoult’s law and the solute obeys Henry’s law.