Chapter: 11th Chemistry : UNIT 7 : Thermodynamics
Solved Numerical Problem: Thermodynamics(Chemistry)
Thermodynamics(Chemistry)
Numerical Problems Questions with Answers, Solution
53. Calculate the work done when 2 moles of an ideal gas expands
reversibly and isothermally from a volume of 500 ml to a volume of 2 L at 25┬░C
and normal pressure.
n
=
2 moles
Vi = 500ml
= 0.5lit
Vf = 2lit
T = 25┬░C
= 298K
w = ŌłÆ2.303
nRT log (Vf / Vi)
w = ŌłÆ2.303
├Ś 2 ├Ś 8.314 ├Ś 298 ├Ś log(2/0.5)
w = ŌłÆ2.303
├Ś 2 ├Ś 8.314 ├Ś 298 ├Ś log(4)
w = ŌłÆ 2.303 ├Ś 2 ├Ś 8.314 ├Ś 298 ├Ś 0.6021
w = ŌłÆ 6871J
w = ŌłÆ 6.871kJ
54. In a constant volume calorimeter, 3.5 g of a gas with
molecular weight 28 was burnt in excess oxygen at 298 K. The temperature of the
calorimeter was found to increase from 298 K to 298.45 K due to the combustion
process. Given that the calorimeter constant is 2.5 kJ KŌłÆ1.
Calculate the enthalpy of combustion of the gas in kJ molŌłÆ1.
Given
Ti
= 298K
Tf
= 298.45K
k
= 2.5 kJKŌłÆ1
m
= 3.5g
Mm
= 28
Heat
evolved = kΔT
=
k(Tf ŌłÆ Ti)
=
2.45 kJKŌłÆ1 ├Ś (298.45 ŌłÆ 298)K
=
1.12 kJ
Heat
evolved for 3.5 g of a gas = 1.12 kJ
Ōł┤ Heat
evolved for 28g of gas ( 1 mole)
=
(1.125├Ś28) / 3.5
The
enthalpy of combustion of the gas
ΔHC
= 9JK molŌłÆ1
55. Calculate the entropy change in the system, and
surroundings, and the total entropy change in the universe during a process in
which 245 J of heat flow out of the system at 77┬░C to the surrounding at 33┬░C.
Given:
Tsys
= 77oC = (77 + 273 ) = 350K
Tsurr
= 33oC = (33 + 273) = 306K
q
= 245J
Solution:
ΔSsys
= q/Tsys = ŌłÆ245 / 350 = ŌłÆ 0.7 JKŌłÆ1
ΔSsurr
= q/Tsys = +245 / 350 = +0.8 JKŌłÆ1
ΔS
= ΔSsys + ΔSsurr
ΔS
univ = ŌłÆ0.7 JKŌłÆ1 + 0.8 JKŌłÆ1
ΔS
univ = ŌłÆ0.1 JKŌłÆ1
56. 1 mole of an ideal gas, maintained at 4.1 atm and at a
certain temperature, absorbs heat 3710J and expands to 2 litres. Calculate the
entropy change in expansion process.
Given:
p = 4.1 atm,
v
= 2 lit,
q
= +3710 J,
n
= 1 mol
Solution:
The
ideal gas equation is

=
( 4.1 atm ├Ś 2 lit ) / ( 0.0821 lit atm molŌłÆ1 KŌłÆ1 ├Ś 1 mol
)
T
= 100 K
ΔSexpansion
= qexpansion / T = 3710J / 100k = 37.1 JKŌłÆ1
ΔSexpansion
= 37.1 JKŌłÆ1
57. 30.4 kJ is required to melt one mole of sodium chloride. The
entropy change during melting is 28.4 JKŌłÆ1 molŌłÆ1 .
Calculate the melting point of sodium chloride.
Given :
ΔHfusion
= 30.4 kJ mol ŌłÆ1
ΔSfusion
= 284.4 JKŌłÆ1 molŌłÆ1
Solution:
ΔSfusion
= ΔHfusion / Tf
Melting
point of NaCl, Tf = ΔHfusion / ΔSfusion
=
30.4 kJ molŌłÆ1 / 28.4 JKŌłÆ1 molŌłÆ1 = ( 30.4 ├Ś
1000 J molŌłÆ1 ) / ( 28.4 JKŌłÆ1 molŌłÆ1)
Melting
point of NaCl, Tf = 1070.4 K
58. Calculate the standard heat of formation of propane, if its
heat of combustion is ŌłÆ2220.2 KJmolŌłÆ1 the heats of formation of CO2
(g) and H2O(1) are ŌłÆ393.5 and ŌłÆ285.8 kJ molŌłÆ1
respectively.
Given
:
ΔH0f
CO2 = ŌłÆ393.5 kJ molŌłÆ1
ΔH0f
H2O = ŌłÆ285.8 kJ molŌłÆ1
ΔH0f
C3H8 = ŌłÆ2220.2 kJ molŌłÆ1
Solution:
Combustion
of propane
C3H8
+ 5O2 ŌåÆ 3CO2 + 4H2O
ΔH0c
= Ōłæ ╬öH0f p ŌłÆ Ōłæ ╬öH0f
r
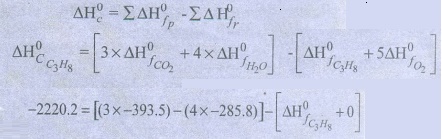
ŌłÆ2220.2 = ŌłÆ1180.5 ŌłÆ 1143.2 ŌłÆ ╬öH0f
C3H8
ΔH0f
C3H8 = ŌłÆ103.5 kJ molŌłÆ1
ΔH0f
C3H8 = ŌłÆ103.5 KJ
59. You are given normal boiling points and standard enthalpies
of vapourisation Calculate the entropy of vapourisation of liquids listed
below.
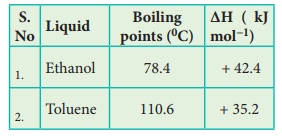
Solution
For
Ethanol:
Given
Tb
=
78.4oC = (78.4 + 273) = 351.4K
ΔHV
(Ethanol) = + 42.4kJ molŌłÆ1
ΔSV
= ΔHV/Tb
ΔSV
= + 42.4kJ molŌłÆ1 / 351.4K
ΔSV
= +42400 J molŌłÆ1 / 351.4K
ΔSV
= +120.66 JKŌłÆ1molŌłÆ1
For
Toluene:
Given
Tb
=110.6┬░C
= (110.6 +273) = 383.6K
ΔHV
(Toluene) = + 35.2 kJ molŌłÆ1
ΔSV
= ΔHV / Tb
ΔSV
= 35.2 kJ molŌłÆ1 / 383.6 K
ΔSV
= +91.76 JKŌłÆ1 molŌłÆ1
60. For the reaction Ag2O(s) ŌĆö> 2Ag(s)
+ ┬Į O2(g) : ╬öH = 30.56 kJ molŌłÆ1 and ╬öS=6.66JKŌłÆ1
molŌłÆ1 (at 1 atm). Calculate the temperature at which ╬öG is equal to zero. Also
predict the direction of the reaction (i) at this temperature and (ii) below
this temperature.
Given:
ΔH
= 30.56 kJmolŌłÆ1
=
30560JmolŌłÆ1
ΔS
= 6.66 ├Ś10ŌłÆ3kJKŌłÆ1mo1ŌłÆ1
T
= ? at which ΔG = 0
ΔG
= ╬öH ŌłÆ T╬öS
0
= ╬öH ŌłÆ T╬öS
T
= ΔH / ΔS
T
= (30.56 kJmolŌłÆ1) / (6.66├Ś10ŌłÆ3 kJKŌłÆ1molŌłÆ1)
T
= 4589K
(i) At 4589K ; ΔG = 0 the reaction is in equilibrium.
(ii)
At temperature below 4589k, ╬öH > T ╬öS ╬öG = ╬öH ŌłÆT ╬öS > 0, the reaction in
the forward direction, is non spontaneous. In other words the reaction occurs
in the backward direction.
61. What is the equilibrium constant Keq for the following
reaction at 400K.
2NOCl Ōćī 2NO(g) + Cl2(g)
given that ΔHo
= 77.2 kJ molŌłÆ1 ; and ╬öS┬░ = 122 JKŌłÆ1
molŌłÆ1
Given:
T
= 400 K
ΔH°c
= 77.2 KJmolŌłÆ1
= 77200 JmolŌłÆ1
ΔG°
= ŌłÆ 2.303RT log Keq
log
Keq = ŌłÆ ╬öG┬░ / 2.303 RT
log
Keq = ŌłÆ (╬öH┬░ ŌłÆ T ╬öS┬░) / 2.303 RT
log
Keq = ŌłÆ ( [77200 ŌĆō 400 ├Ś 122] / [2.303 ├Ś 8.314 ├Ś 400] )
log
Keq = ŌłÆ (28400 / 7659)
log
Keq = ŌłÆ 3.7080
Keq
= antilog (ŌłÆ3.7080)
Keq
= 1.95 ├Ś10-4
62. Cyanamide (NH2CN) is completely burnt in excess
oxygen in a bomb calorimeter, ╬öU was found to be -742.4 kJ molŌłÆ1,
calculate the enthalpy change of the
reaction at 298K. NH2CN(s) + 3/2 O2(g) ŌåÆ N2 (g) + CO2 (g) + H2O(l) ╬öH= ?
Given
T
= 298K; ╬ö U= ŌłÆ742.4kJmolŌłÆ1
ΔH
= ?
Solution:
ΔH
= ΔU + ΔngRT
ΔH
= ╬öU+ (np ŌłÆ nr) RT
ΔH
= -742.4 + (2- 3/2) ├Ś 8.314 ├Ś l0ŌłÆ3 ├Ś 298
=
ŌłÆ742.4 + (0.5 ├Ś 8.314 ├Ś 10ŌłÆ3 ├Ś 298)
=
ŌłÆ742.4 + 1.24
=
ŌłÆ741.16 kJmolŌłÆ1
63. Calculate the enthalpy of hydrogenation of ethylene from the
following data. Bond energies of C-H, C-C, C = C and H - H are 414, 347, 618
and 435 kJ molŌłÆ1
Given:
EC-H
= 414kJ molŌłÆ1
Ec-c
= 347 kJ molŌłÆ1
Ec-c
= 618kJ molŌłÆ1
EH-H
= 435 kJ molŌłÆ1
Solution:
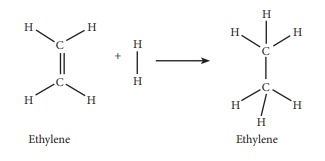
ΔHr
= Ōłæ(Bond energy)r ŌłÆ Ōłæp (Bond energy)p
ΔHr
= (Ec-c + 4EC-H + EH-H) ŌłÆ (Ec-c +
6EC-H)
ΔHr
= (618 + (4 ├Ś 414) = 435) ŌłÆ (347 + (6 ├Ś 414))
ΔHr
= 2709 ŌłÆ 2831
ΔHr
= ŌłÆ122 kJ molŌłÆ1
64. Calculate the lattice energy of CaCl2 from the
given data
Ca (s)+Cl2(g) ŌåÆ CaCl2(s) ŌłåH0f
= ŌłÆ 795 kJ molŌłÆ1
Ca(s) +
Cl2(g) ŌåÆ CaCl2(s) ╬öH┬░f = ŌłÆ795 kJ molŌłÆ1
Atomisation : Ca(s)
ŌåÆ Ca(g) ╬öH┬░1 = +121 kJ molŌłÆ1
Ionisation: Ca(g)
ŌåÆ Ca2+(g) + 2eŌłÆ ╬öH┬░2 = +2422 kJ molŌłÆ1
Dissociation : Cl2(g)
ŌåÆ 2Cl(g) ╬öH┬░3 = +242.8 kJ molŌłÆ1
Electron affinity :
Cl(g) + eŌłÆ ŌåÆ ClŌłÆ(g)
╬öH┬░4 = ŌłÆ355 kJ molŌłÆ1
Solution:

ΔHf
= ΔH1 + ΔH2 + ΔH3 + 2 ΔH4 + u
ŌłÆ795
= 121 + 2422 + 242.8 + (2 ├Ś ŌłÆ355) + u
ŌłÆ795
= 2785.8 ŌłÆ 710 + u
ŌłÆ795
= 2075.8 + u
u
= ŌłÆ 795 ŌłÆ 2075.8
u
= ŌłÆ2870.8 kJ molŌłÆ1
65. Calculate the enthalpy change for the reaction Fe2O3
+ 3CO ŌåÆ 2Fe + 3CO2 from the following data.
2Fe + 3/2 O2
ŌåÆ Fe2O3; ╬öH = -741kJ
C + 1/2 O2
ŌåÆ CO; ╬öH = ŌłÆ137kJ
C+ O2 ŌåÆ
CO2; ╬öH = ŌłÆ 394.5kJ
┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬Ł┬ŁGiven :
ΔHf
(Fe2O3) = ŌłÆ 741kJmolŌłÆl
ΔHf
(CO) = ŌłÆ 137kJmolŌłÆ1
ΔHr
= ?
Solution:
Fe2O3
+3CO ŌåÆ 2Fe + 3CO2
ΔHr
= Ōłæ( ╬öHf) products ŌłÆ Ōłæ (╬öHf )reactants
ΔHr
= [0+ 3(ŌłÆ 394.5)] ŌłÆ [ŌłÆ741 + 3(ŌłÆ 137)]
ΔHr
= [ŌłÆ1183.5] ŌłÆ [ŌłÆ1152]
ΔHr
= ŌłÆ1183.5 + ŌłÆ1152
ΔHr
= ŌłÆ31.5 kJ molŌłÆ1
66. When 1-pentyne (A) is treated with 4N alcoholic KOH at 175┬░C, it is
converted slowly into an equilibrium mixture of 1.3% 1-pentyne (A), 95.2%
2-pentyne (B) and 3.5% of 1,2 pentadiene (C) the equilibrium was maintained at
175°C, calculate ΔG0 for the following equilibria.
B Ōćī A ╬öG01
= ?
B Ōćī C ╬öG02
= ?
Given
:
T=
175┬░ C = 175 + 273 = 448K
Concentration
of 1-pentyne [A] = 1.3%
Concentration
of 2-pentyne [B] = 95.2%
Concentration
of 1, 2-pentadiene [C] = 3.5%
B
[95.2%] Ōćī A [3.5%]
K1
= 1.3 / 95.2 = 0.0136
B [95.2%]
Ōćī C [3.5%]
K2
= 3.5 / 95.2 = 0.0367
ŌćÆ ╬öG01
= ŌłÆ2.303 RT logK1
ΔG01
= ŌłÆ2.303 ├Ś 8.314 ├Ś 448 ├Ś log0.0136
ΔG01
= ŌłÆ2.303 ├Ś 8.314 ├Ś 448 ├Ś ŌłÆ1.8664
ΔG01
= +16010J
ΔG01
= +16 kJ
ΔG02
= ŌłÆ2.303 RT logK2
ΔG02
= ŌłÆ2.303 ├Ś 8.314 ├Ś 448 ├Ś log 0.0367
ΔG02
= ŌłÆ2.303 ├Ś 8.314 ├Ś 448 ├Ś ŌłÆ1.4353
ΔG02
= +12312 J
ΔG02
= +12.312 kJ
67. At 33K, N2O4 is fifty percent
dissociated, calculate the standard free energy change at this temperature and
at one atmosphere
Given:
N2O4
Ōćī 2NO2
Initial
mole 1
At
Equilibrium remaining mole
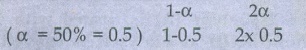
Total
moles at equilibrium 0.5 + 1 = 1.5
Total
pressure = 1atm
Partial
pressure = mole fraction ├Ś total pressure
PN2O4
= (0.5/1.5) ├Ś 1 = 0.5 / 1.5
PNO2
= (1/1.5) ├Ś 1 = 1/ 1.5
KP
= PNO2 / PN2O4 = (1/1.5)2 / (0.5/1.5) = 1.33
We
know that,
ΔG°
= ŌłÆ2.303RT log Keq
= ŌłÆ2.303 ├Ś 8.314 ├Ś 331og 1.33
= ŌłÆ2.303 ├Ś 8.314 ├Ś 33 ├Ś 0.1239
ΔG°
= ŌłÆ78.29JmolŌłÆ1
[Alternative
Answer]

68. The standard enthalpies of formation of SO2and SO3are
ŌłÆ297 kJ molŌłÆ1 and ŌłÆ396 kJ molŌłÆ1 respectively. Calculate
the standard enthalpy of reaction for the reaction: SO2 + ┬Į O2 ŌåÆ
SO3
Given:
ΔHof
(SO2) = ŌłÆ297 kJ molŌłÆ1
ΔHof
(SO2) = ŌłÆ396 kJ molŌłÆ1
SO2
+ ┬Į O2 ŌåÆ SO3
ΔHo1
= ?
Solution:
ΔHor
= (ΔHof)compound
ŌłÆ Ōłæ (╬öHf)elements
ΔHor
= ╬öHof (SO3) ŌłÆ ( ╬öHof
(SO2) + 1/2 ΔHof (O2) )
ΔHor
= ŌłÆ396 kJ molŌłÆ1
= ŌłÆ (ŌłÆ297kJ molŌłÆ1 + 0)
ΔHor
= ŌłÆ396 kJ molŌłÆ1 + 297
ΔHor
= ŌłÆ 99kJ molŌłÆ1
69. For the reaction at 298 K: 2A +B ŌĆö> C
╬öH = 400 J molŌłÆ1; ╬öS = 0.2 JKŌłÆ1molŌłÆ1
Determine the temperature at which the reaction would be
spontaneous.
Given :
ΔH
= 400 J molŌłÆ1
ΔS
= 0.2 J KŌłÆ1 molŌłÆ1
T
= 298 K
Solution:
We
know that ╬öG = ╬öH ŌłÆ T╬öS
At
equilibrium, ΔG = 0
Ōł┤ T╬öS = ╬öH
T
= ╬öH / ╬öS = ( 400 J molŌłÆ1 ) / ( 0.2 JkŌłÆ1 molŌłÆ1)
T = 2000K
ΔG
= 400 ŌłÆ (2000 ├Ś 0.2)
= 0
if
T > 2000K ΔG will be negative
The
reaction would be spontaneous only beyond 2000K
70.
Find out the value of equilibrium constant for the following reaction at 298K, 2NH3(g) + CO2(g) Ōćī NH2CONH2(aq) + H2O (1) Standard Gibbs
energy change, ╬öGr0 at the given temperature is ŌłÆ13.6 kJ molŌłÆ1.
Solution :
Given:
T = 298K
ΔGr0
= ŌłÆ13.6 kJ molŌłÆ1
╬öG0 = ŌłÆ2.303
RT log Keq
log Keq = ŌłÆ╬öG0 / 2.303RT
log Keq = [ŌłÆ(ŌłÆ13.6)] / [2.303 ├Ś 8.314├Ś10ŌĆō3 ├Ś 298]
log Keq =
2.38
Keq = antilog
(2.38)
Keq = 239.88
71. A gas mixture of 3.67 lit of ethylene and methane on
complete combustion at 25┬░C and at 1 atm pressure produce 6.11 lit of
carbondioxide. Find out the amount of heat evolved in kJ, during this
combustion. (╬öHc(CH4) = - 890 kJ molŌłÆ1 and (╬öHc(C2H4)
= ŌłÆ1423 kJ molŌłÆ1
Solution:
ΔHC
(CH4) = ŌłÆ 890 kJ molŌłÆ1
ΔHC
(C2H4) = ŌłÆ 1423 kJ molŌłÆ1
Let
the mixture contain x lit of CH4 and (3.67 ŌłÆ x) lit of ethylene.
CH4
+ 2O2 ŌåÆ CO2 + 2H2O
x lit x lit
C2H4
+ 3O2 ŌåÆ 2CO2 + 2H2O
(3.67-x)
lit 2 (3.67 - x) lit
Volume
of Carbondioxide formed
=
x + 2 (3.67ŌłÆ x) = 6.11 lit
x
+ 7.34 ŌłÆ 2x = 6.11
7.34
- x = 6.11
x
= 1.23 lit
Given
mixture contains 1.23 lit of methane and 2.44 lit of ethylene, hence
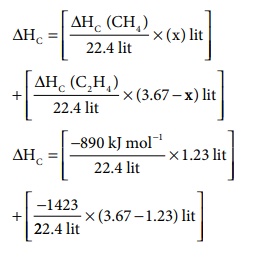
ΔHc
= [(╬öHc (CH4) / 22.4) ├Ś (x)] + [ (╬öHc (C2H4)
/ 22.4) ├Ś (3.67 - x) ]
ΔHc
= [ (ŌłÆ890kJmolŌłÆ1 / 22.4) ├Ś 1.23] + [ (ŌłÆ1423/22.4) ├Ś (3.67 ŌłÆ 1.23) ]
ΔH
= [ ŌłÆ48.87kJmolŌłÆ1] + [ŌłÆ155kJmolŌłÆ1]
ΔHc
= ŌłÆ203.87 kJmolŌłÆ1
Problem
The standard enthalpies of formation of C2H5OH(l), CO2(g) and H2O(l) are - 277, -393.5 and -285.5 kJ mol-1 respectively.
Calculate the standard enthalpy change for the reaction
C2H5OH(l)+3O2(g) ŌåÆ2CO2(g)+ 3 H2O(l)
The enthalpy of formation of O2(g) in the standard state is Zero, by definition
Solution:
For example, the standard enthalpy change for the combustion of ethanol can be calculated from the standard enthalpies of formation of C2H5OH(l), CO2(g) and H2O(l). The enthalpies of formation are ŌĆō277, ŌĆō 393.5 and ŌĆō285.5 kJ molŌĆō1 respectively.
C3H5OH(l) + 3O2(g) ŌåÆ 2CO2(g) + 3H2O(l)

=[ ŌłÆ787 ŌłÆ 856 . 5] ŌłÆ [ ŌłÆ277]
= - 1643 .5 + 277
ŌłåH0r = ŌłÆ1366 . 5 KJ
Problem
Calculate the value of ŌłåU and ŌłåH on heating 128.0 g of oxygen from 0o C to 1000 C. CV and CP on an average are 21 and 29 J mol-1 K-1. (The difference is 8Jmol-1 K-1 which is approximately equal to R)
Solution.
We know
ŌłåU = n Cv (T2-T1)
ŌłåH = n CP (T2- T1)
Here
n= 128/32 4 moles ;
T2 = 1000
C =373K;
T1 = 00
C = 273K
ŌłåU = n Cv (T2-T1)
ŌłåU = 4 x 21 x (373 - 273)
ŌłåU = 8400 J
ŌłåU = 8.4 kJ
ŌłåH = n Cp (T2- T1)
ŌłåH = 4 ├Ś 29 ├Ś (373- 273)
ŌłåH = 11600 J
ŌłåH = 11.6 kJ
Problem:
If an automobile engine burns petrol at a temperature of 816o C and if the surrounding temperature is 21o C, calculate its maximum possible efficiency.
Solution:
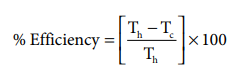
Here
Th = 816+273= 1089 K;
Tc= 21+273= 294K
%Efficiency=( 1089-294 / 1089) x100
%Efficiency=73%
Problem:
Calculate the standard entropy change for the following reaction( ŌłåS0f ), given the standard entropies of CO2(g), C(s),O2(g) as 213.6 , 5.740 and 205 JKŌłÆ1 respectively.
C(g) + O2(g) ŌåÆCO2(g)
S0r = Ōłæ S0products ŌłÆ Ōłæ Sreac0 tan ts
S0r = {S0CO 2 } ŌłÆ {SC0 + S0O2 }
S0r = 213.6 ŌłÆ [5.74 + 205]
S0r = 213.6 ŌłÆ[210.74]
S0r = 2.86 JKŌłÆ1
Problem:
Calculate the entropy change during the melting of one mole of ice into water at 00 C and 1 atm pressure. Enthalpy of fusion of ice is 6008 J mol-1
Given:
ŌłåHfusion = 6008 JmolŌłÆ1
Tf = 0 0
C = 273 K
H 2O(S) --273 KŌåÆ H 2O ( l)

S fusion = 22 .007 J K ŌłÆ1 moleŌłÆ1
Problem:

Calculate ╬öG0 for conversion of oxygen to ozone 3/2 O2 Ōåö O3(g) at 298 K, if Kp for this conversion is 2.47 u 10ŌłÆ29 in standard pressure units.
Solution:
╬öG0 = ŌłÆ 2.303 RT log Kp
Where
R = 8.314 JKŌłÆ1molŌłÆ1
Kp = 2.47 x10ŌłÆ29
T = 298K
╬öG0=ŌłÆ2.303(8.314)(298)log(2.47u10ŌłÆ29)
╬öG0 = 16300 JmolŌłÆ1
╬öG0 = 16.3 KJ molŌłÆ1
Related Topics