Logic gates

DIGITAL ELECTRONICS

Logic gates

A logic gate is an electronic circuit which functions based on digital signals. The logic gates are considered as the basic building blocks of most of the digital systems. It has one output with one or more inputs. There are three types of basic logic gates: AND, OR, and NOT. The other logic gates are Ex-OR, NAND, and NOR. They can be constructed from the basic logic gates.

Digital electronics deals with logical operations. The variables are called logical variables. The operators like logical addition (+) and logical multiplication (.) are called logical operators. When the logical operators (+, .) operate on logical variables (A, B), it gives logical constant (Y). The equation that represents this operation is called logical statement.

For example,

Logical operator: +

Logical variable: A, B

Logical constant: Y

Logical Statement: Y = A + B

The possible combinations of inputs and the corresponding output is given in table called truth table. The circuits which perform the basic logical operations such as logical addition, multiplication and inversion are discussed below.

AND gate

Circuit symbol

The circuit symbol of a two input AND gate is shown in Figure 9.41(a). A and B are inputs and Y is the output. It is a logic gate and hence A, B, and Y can have the value of either 1 or 0.

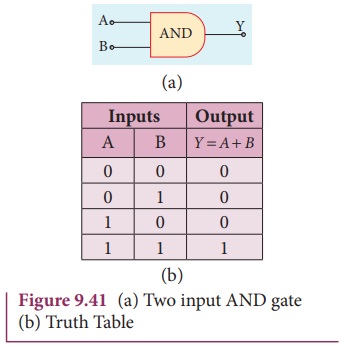
Boolean equation:

Y = A. B

It performs logical multiplication and is different from arithmetic multiplication.

Logic operation

The output of AND gate is high (1) only when all the inputs are high (1). The rest of the cases the output is low. Hence the output of AND gate is high (1) only when all the inputs are high. It is represented in the truth table (Figure 9.41(b)).

OR gate

Circuit Symbol

The circuit symbol of a two input OR gate is shown in Figure 9.42(a). A and B are inputs and Y is the output.

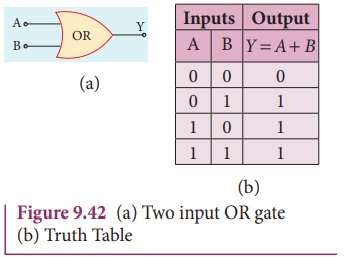
Boolean equation:

Y = A + B

It performs logical addition and is different from arithmetic addition.

Logic operation

The output of OR gate is high (logic 1 state) when either of the inputs or both are high. The truth table of OR gate is shown in Figure 9.42(b).

NOT gate

Circuit symbol

The circuit symbol of NOT gate is shown in Figure 9.43(a). A is the input and Y is the output.

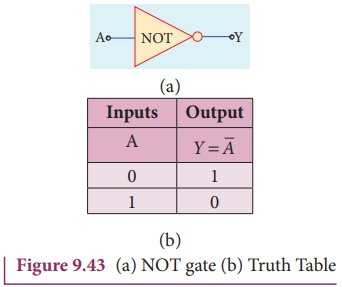
Boolean equation

Y = 

Logic operation

The output is the complement of the input. It is represented with an overbar. It is also called as inverter. The truth table infers that the output Y is 1 when input A is 0 and vice versa. The truth table of NOT is shown in Figure 9.43(b).

NAND gate

The circuit symbol of NAND gate is shown in Figure 9.44(a). A and B are inputs and Y is the output.

Boolean equation

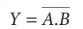
Logic operation

The output Y equals the complement of AND operation. The circuit is an AND gate followed by a NOT gate. Therefore, it is summarized as NAND. The output is at logic zero only when all the inputs are high. The rest of the cases, the output is high (Logic 1 state). The truth table of NAND gate is shown in Figure 9.44(b).

NOR gate

Circuit symbol

The circuit symbol of NOR gate is shown in Figure 9.45(a). A and B are inputs and Y is the output.

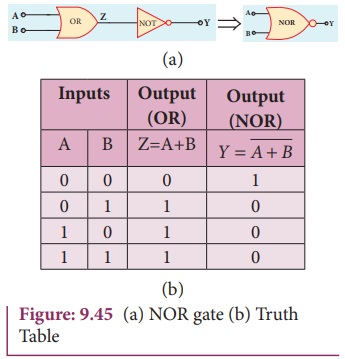
Boolean equation

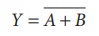
Logic operation

Y equals the complement of OR operation (A OR B). The circuit is an OR gate followed by a NOT gate and is summarized as NOR.

The output is high when all the inputs are low. The output is low for all other combinations of inputs. The truth table of NOR gate is shown in Figure 9.45(b).

Ex-OR gate

Circuit symbol

The circuit symbol of Ex-OR gate is shown in Figure 9.46(a). A and B are inputs and Y is the output. The Ex-OR operation is denoted as .

Boolean equation

Logic operation

The output is high only when either of the two inputs is high. In the case of an Ex-OR gate with more than two inputs, the output will be high when odd number of inputs are high. The truth table of Ex-OR gate is shown in Figure 9.46(b).

EXAMPLE 9. 11

What is the output Y in the following circuit, when all the three inputs A, B, and C are first 0 and then 1?

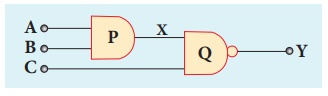
Solution

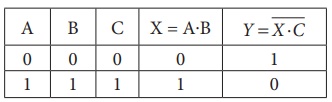
EXAMPLE 9. 11

In the combination of the following gates, write the Boolean equation for output Y in terms of inputs A and B.

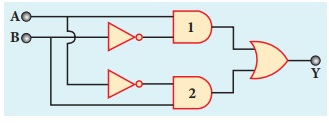
Solution

The output at the 1st AND gate: A

The output at the 2nd AND gate: B 

The output at the OR gate: Y = A.  + . B