Solving Quadratic Equations by factorization method

Solving Quadratic Equations

We have already learnt how to solve linear equations in one, two and three variable(s). Recall that the values of the variables which satisfies a given equation are called its solution(s). In this section, we are going to study three methods of solving quadratic equation, namely factorization method, completing the square method and using formula.

Solving a quadratic equation by factorization method.

We follow the steps provided below to solve a quadratic equation through factorization method.

Step 1 Write the equation in general form ax² + bx +c = 0

Step 2 By splitting the middle term, factorize the given equation.

Step 3 After factorizing, the given quadratic equation can be written as product of two liner factory.

Step 4 Equate each linear factor to zero and solve for x. 

These values of x gives the roots of the equation.

Example 3.27

Solve 2x² − 2√6 x + 3 = 0

Solution 

2x² − 2√6 x + 3 = 2x² − √6 x − √6x + 3 (by spliting the middle term)

=√2x (√2x − √3 ) − √3 (√2x − √3)= (√2x − √3)( √2x − √3)

Now, equating the factors to zero we get,

(√2x − √3)( √2x − √3)=0

√2x − √3 = 0 or √2x − √3 = 0

√2x = √3 or √2x = √3

Therefore the solution is x = √3/√2 .

Example 3.28

Solve 2m² + 19m + 30 = 0

Solution

2m ² + 19m + 30 = 2m ² + 4m + 15m + 30 = 2m(m + 2) + 15(m + 2)

= (m + 2)(2m + 15)

Now, equating the factors to zero we get,

(m + 2)(2m + 15) = 0

m + 2 = 0  gives, m = – 2  or 2m + 15 = 0  we get, m = -15/2

Therefore the roots are -2 , -15/2

Some equations which are not quadratic can be solved by reducing them to quadratic equations by suitable substitutions. Such examples are illustrated below.

Example 3.29

Solve x⁴ − 13x² + 42 = 0

Solution

Let x² = a. Then, (x²)² − 13x² + 42 = a² −13a + 42 = (a − 7)(a − 6)

Given, (a − 7)(a − 6) = 0 we get, a = 7 or 6.

Since a = x² , x²  = 7 then, x= ± √7 or x² = 6 we get, x = ± √6

Therefore the roots are x = ± √7 , ± √6

Example 3.30

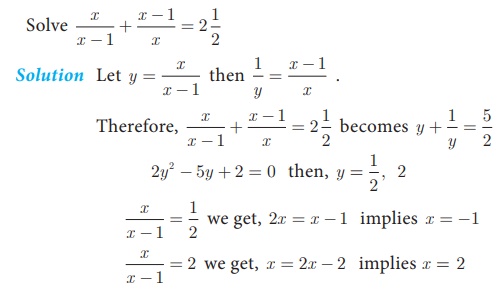
Therefore, the roots are x = −1 , 2.