Expression, Zeroes, Roots, Formation, Example, Solution | Algebra - Quadratic Equations | 10th Mathematics : UNIT 3 : Algebra
Chapter: 10th Mathematics : UNIT 3 : Algebra
Quadratic Equations
Quadratic
Equations
Introduction
Arab mathematician
Abraham bar Hiyya Ha-Nasi, often known by the Latin name Savasorda, is famed
for his book ‘Liber Embadorum’ published in 1145 AD(CE) which is the first book
published in Europe to give the complete solution of a quadratic equation.
For a period of more
than three thousand years beginning from early civilizations to current times,
humanity knew how to solve a general quadratic equation in terms of its
co-efficients by using four arithmetical operations and extraction of roots.
This process is called “Solving by Radicals”. Huge amount of research has been
carried to this day in solving various types of equations.
Quadratic Expression
An expression of degree n
in variable x is a0xn+ a1xn−1+a2xn−2+ ... +an-1x +an
where a0 ≠0 and a1
, a2,...an are real numbers. a 0
, a1, a 2 , ... an are
called coefficients of the expression.
In particular an
expression of degree 2 is called a Quadratic Expression which is expressed as p(x)
= ax 2 +bx +c, a ≠0 and a, b,
c are real numbers.
1. Zeroes of a Quadratic Polynomial
Let p(x)
be a polynomial. x=a is called zero of p(x) if p(a)
= 0
For example, if p(x)
= x2–2x–8 then p(–2)=4+4–8 = 0 and p(4) =
16– 8 –8 = 0
Therefore –2 and 4 are
zeros of the polynomial p(x) = x2–2x–8.
2. Roots of Quadratic Equations
Let ax2
+ bx +c = 0, (a ≠ 0) be a quadratic equation. The values of
x such that the expression ax 2 + bx + c becomes
zero are called roots of the quadratic equation ax 2 + bx +c
= 0 .
We have, ax 2
+ bx + c = 0

3. Formation of a Quadratic Equation
If a and b
are roots of a quadratic equation ax2 + bx +c =
0 then
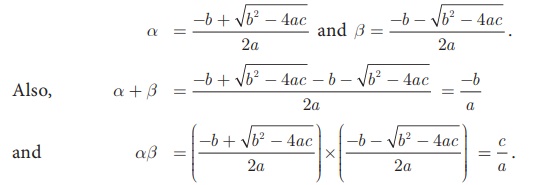
Since, (x - a)
and (x - b) are factors of ax2 + bx +c
= 0 ,
We have (x - α)(x
- β) = 0
Hence, x 2
− (α + β)x + αβ = 0
That is, x2 - (sum of roots) x + product of roots = 0 is the general form of
the quadratic equation when the roots are given.
Example 3.24
Find the zeroes of the
quadratic expression x2 + 8x + 12.
Solution
Let p(x)= x2
+ 8x + 12 =(x+2)(x+6)
p(–2)= 4 – 16 + 12=0
p(–6)= 36 – 48 + 12=0
Therefore –2 and –6 are
zeros of p(x)= x2 + 8x + 12
Example 3.25
Write down the quadratic
equation in general form for which sum and product of the roots are given below.
(i) 9, 14
(ii) – 7/2 , 5/2
(iii) – 3/5 , - 1/2
Solution
(i) General form of the
quadratic equation when the roots are given is x2 -
(sum of the roots ) x + product of the roots = 0
x 2 − 9x +
14 = 0
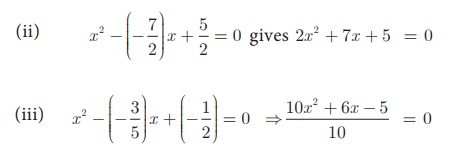
Therefore, 10x 2
+ 6x − 5 = 0.
Example 3.26
Find the sum and product
of the roots for each of the following quadratic equations :
(i) x 2
+ 8x − 65 = 0
(ii) 2x2
+ 5x + 7 = 0
(iii) kx 2
− k 2 x − 2k 3 =
0
Solution
Let a and b be the roots of the
given quadratic equation
x 2 + 8x − 65
= 0
a = 1, b = 8,
c = –65
α + β = −b/a
= –8 and αβ = c/a = –65
α + β = −8 ;
αβ = −65
(ii) 2x 2
+ 5x + 7 = 0
a = 2, b = 5,
c = 7
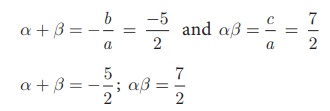
(iii)
kx 2 − k
2 x − 2k 3 = 0
a = k, b =
-k2 , c = –2k3
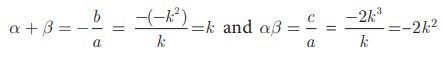
Related Topics