Explanation, Formulas, Solved Example Problems | KirchhoffŌĆÖs rule - WheatstoneŌĆÖs bridge | 12th Physics : Current Electricity
Chapter: 12th Physics : Current Electricity
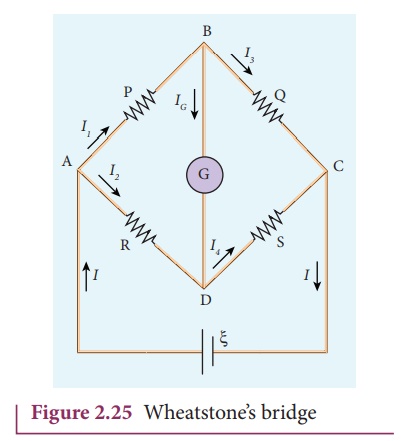
WheatstoneŌĆÖs bridge
WheatstoneŌĆÖs
bridge
An important application
of KirchhoffŌĆÖs rules is the WheatstoneŌĆÖs bridge. It is used to compare
resistances and also helps in determining the unknown resistance in electrical
network. The bridge consists of four resistances P, Q, R and S connected as
shown in Figure 2.25. A galvanometer G is connected between the points B and D.
The battery is connected between the points A and C. The current through the
galvanometer is IG and its resistance is G.
Applying KirchhoffŌĆÖs
current rule to junction B

Applying
KirchhoffŌĆÖs current rule
to junction D,

Applying KirchhoffŌĆÖs
voltage rule to loop ABDA,
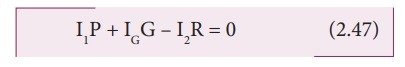
Applying KirchhoffŌĆÖs
voltage rule to loop ABCDA,
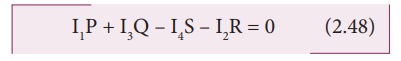
When the points B and D
are at the same potential, the bridge is said to be balanced. As there is no
potential difference between B and D, no current flows through galvanometer (IG
= 0). Substituting IG = 0 in equation (2.45), (2.46) and (2.47), we
get

Substituting
the equation (2.49) and (2.50) in equation (2.48)
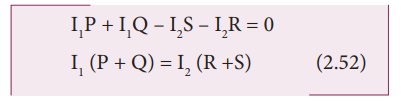
Dividing equation (2.52)
by equation (2.51), we get
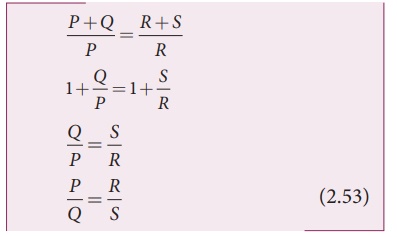
This is the bridge
balance condition. Only under this condition, galvanometer shows null
deflection. Suppose we know the values of two adjacent resistances, the other
two resistances can be compared. If three of the resistances are known, the
value of unknown resistance (fourth one) can be determined.
EXAMPLE 2.23
In a WheatstoneŌĆÖs bridge P = 100 ╬®, Q = 1000 ╬® and R = 40 ╬®. If the galvanometer shows zero deflection, determine the value of S.
Solution
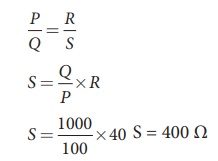
EXAMPLE 2.24
What is
the value of x when the WheatstoneŌĆÖs
network is balanced?
P = 500
╬®, Q = 800 ╬®, R = x + 400, S = 1000 ╬®

Solution
P/Q = R/S
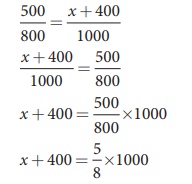
x + 400 =
0.625 ├Ś 1000
x + 400 =
625
x = 625 ŌĆō
400
x = 225 ╬®
Related Topics