Chapter: 12th Physics : Current Electricity
OhmŌĆÖs Law: Solved Example Problems
OHMŌĆÖS LAW: Solved Example Problems
EXAMPLE 2.5
A potential difference across 24 ╬® resistor is 12 V. What is the current through the resistor?
Solution
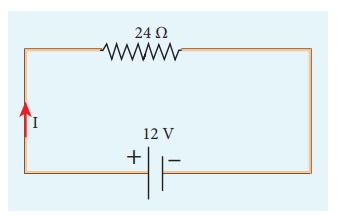
V = 12 V and R = 24 ╬®
Current, I = ?
From OhmŌĆÖs law, I = V/R = 12/24 = 0 .5 A
Resistivity: Solved Example Problems
EXAMPLE 2.6
The resistance of a wire is 20 ╬®. What will be new resistance, if it is stretched uniformly 8 times its original length?
Solution
R1 = 20 ╬®, R2= ?
Let the original length (l1) be l.
The new length, l2 = 8l1 (i.,e) l2 =8l
The original resistance, R = Žü [ l1 / A1]
The new resistance
R2 = 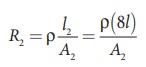
Though the wire is stretched, its volume is unchanged.
Initial volume = Final volume
A1l1= A2l2 , A1l = A28l
A1 / A2 = 8l / l = 8
By dividing equation R2 by equation R1, we get

Substituting the value of A1/A2, we get
R2 / R1 = 8 ├Ś8 = 64 2
R2 = 64 ├Ś 20=1280 ╬®
Hence, stretching the length of the wire has increased its resistance.
EXAMPLE 2.7
Consider a rectangular block of metal of height A, width B and length C as shown in the figure.
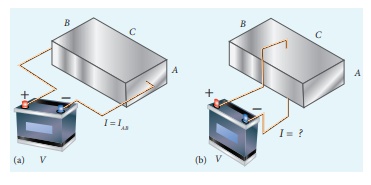
If a potential difference of V is applied between the two faces A and B of the block (figure (a)), the current IAB is observed. Find the current that flows if the same potential difference V is applied between the two faces B and C of the block (figure (b)). Give your answers in terms of IAB.
Solution
In the first case, the resistance of the block

Resistors in series and parallel:
EXAMPLE 2.8
Calculate the equivalent resistance for the circuit which is connected to 24 V battery and also find the potential difference across 4 ╬® and 6 ╬® resistors in the circuit.
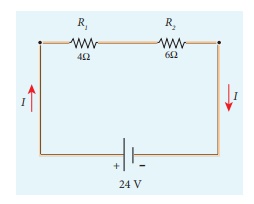
Solution
Since the resistors are connected in series, the effective resistance in the circuit
= 4 ╬® + 6 ╬® = 10 ╬®
The Current I in the circuit= V/ Req = 24/10 = 2 .4 A
Voltage across 4╬® resistor
V1 = IR1 = 2 . 4 A├Ś 4 ╬® = 9.6V
Voltage across 6 ╬® resistor
V2 = IR1 = 2 . 4 A├Ś 6 ╬® =14 .4V
EXAMPLE 2.9
Calculate the equivalent resistance in the following circuit and also find the current I, I1 and I2 in the given circuit.
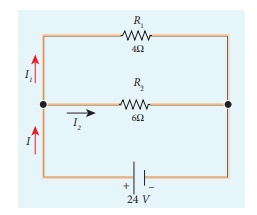
Solution
Since the resistances are connected in parallel, therefore, the equivalent resistance in the circuit is
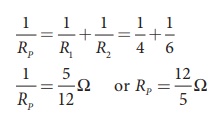
The resistors are connected in parallel, the potential (voltage) across each resistor is the same.
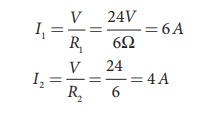
The current I is the total of the currents in the two branches. Then,
I = I1 + I2= 6 A + 4 A = 10 A
EXAMPLE 2.10
When two resistances connected in series and parallel their equivalent resistances are 15 ╬® and 56/15 ╬® respectively. Find the individual resistances.
Solution
Rs = R1 + R2 = 15 ╬® (1)

The above equation can be solved using factorisation.
R12-8 R1-7 R1+ 56 = 0
R1 (R1ŌĆō 8) ŌĆō 7 (R1ŌĆō 8) = 0
(R1ŌĆō 8) (R1ŌĆō 7) = 0
If (R1= 8 ╬®)
using in equation (1)
8 + R2 = 15
R2 = 15 ŌĆō 8 = 7 ╬® ,
R2 = 7 ╬® i.e , (when R1 = 8 ╬® ; R2 = 7 ╬®)
If (R1= 7 ╬®)
Substituting in equation (1)
7 + R2 = 15
R2 = 8 ╬® , i.e , (when R1 = 8 ╬® ; R2 = 7 ╬® )
EXAMPLE 2.11
Calculate the equivalent resistance between A and B in the given circuit.
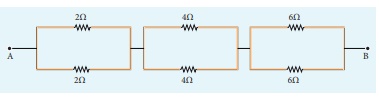
Solution
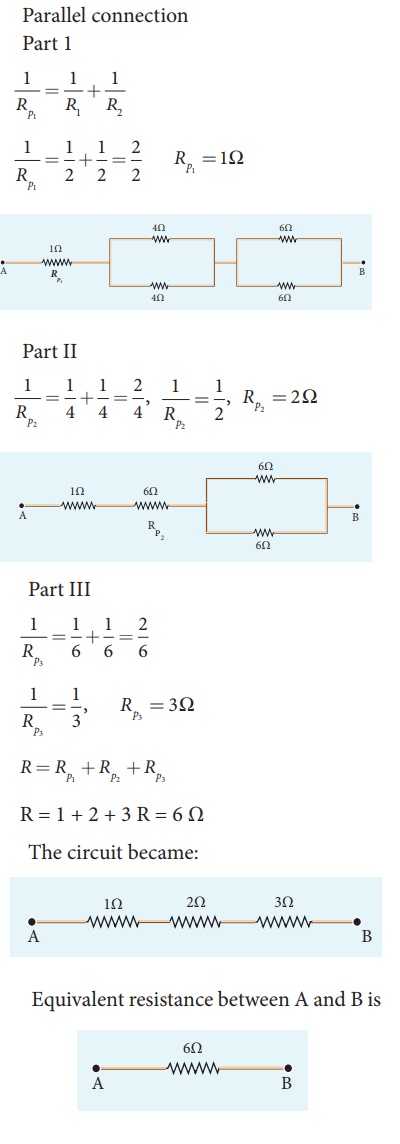
EXAMPLE 2.12
Five resistors are connected in the configuration as shown in the figure. Calculate the equivalent resistance between the points a and b.
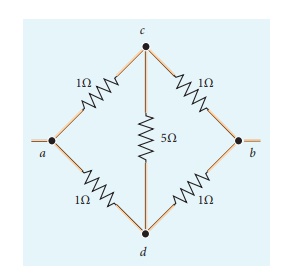
Solution
Case (a)
To find the equivalent resistance between the points a and b, we assume that current is entering the junction a. Since all the resistances in the outside loop are the same (1╬®), the current in the branches ac and ad must be equal. So the electric potential at the point c and d is the same hence no current flows into 5 ╬® resistance. It implies that the 5 ╬® has no role in determining the equivalent resistance and it can be removed. So the circuit is simplified as shown in the figure.
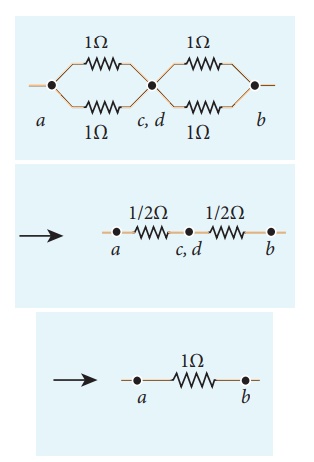
The equivalent resistance of the circuit between a and b is Req = 1╬®
Temperature dependence of resistivity: Solved Example Problems
EXAMPLE 2.13
If the resistance of coil is 3 ╬® at 20 0C and ╬▒ = 0.004/0C then determine its resistance at 100 0C.
Solution
R0= 3 ╬®,ŌĆā T = 100┬║C,ŌĆā T0 = 20┬║C
╬▒ = 0.004/┬║C,ŌĆā RT = ?
RT= R0(1 + ╬▒(T-T0))
R100 = 3(1 + 0.004 ├Ś 80)
R100 = 3(1 + 0.32)
R100 = 3(1.32)
R100 = 3.96 ╬®
EXAMPLE 2.14
Resistance of a material at 10┬║C and 40┬║C are 45 ╬® and 85 ╬® respectively. Find its temperature co-efficient of resistance.
Solution
T0 = 10┬║C, T = 40┬║C, R0= 45 ╬® , R = 85 ╬®
α = 1/R . ΔR /ΔT

╬▒ = 0.0296 per ┬║C
Related Topics