Temperature dependence of resistivity

Temperature dependence of resistivity

The resistivity of a material is dependent on temperature. It is experimentally found that for a wide range of temperatures, the resistivity of a conductor increases with increase in temperature according to the expression,

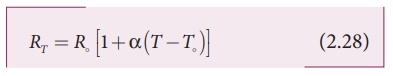
where ρT is the resistivity of a conductor at T oC, ρo is the resistivity of the conductor at some reference temperature Tº (usually at 20ºC) and α is the temperature coefficient of resistivity. It is defined as the ratio of increase in resistivity per degree rise in temperature to its resistivity at Tº.

From the equation (2.27), we can write

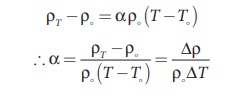
where ∆ρ = ρT – ρo is change in resistivity for a change in temperature ∆T = T – To. Its unit is per oC.

α of conductors

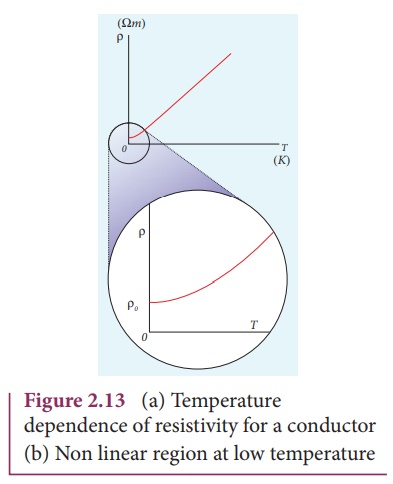
For conductors α is positive. If the temperature of a conductor increases, the average kinetic energy of electrons in the conductor increases. This results in more frequent collisions and hence the resistivity increases. The graph of the equation (2.27) is shown in Figure 2.13

Even though, the resistivity of conductors like metals varies linearly for wide range of temperatures, there also exists a non-linear region at very low temperatures. The resistivity approaches some finite value as the temperature approaches absolute zero as shown in Figure 2.13(b).

As the resistance is directly proportional to resistivity of the material, we can also write the resistance of a conductor at temperature T ºC as

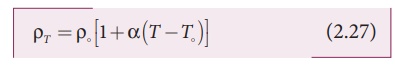
The temperature coefficient can be also be obtained from the equation (2.28),

where          R = RT −R is change in resistance during the change in temperature  ΔT = T –T

α of of semiconductors

For semiconductors, the resistivity decreases with increase in temperature. As the temperature increases, more electrons will be liberated from their atoms (Refer unit 9 for conduction in semi conductors). Hence the current increases and therefore the resistivity decreases as shown in Figure 2.14. A semiconductor with a negative temperature coefficient of resistance is called a thermistor.

The typical values of temperature coefficients of various materials are given in table 2.3.

We can understand the temperature dependence of resistivity in the following way. In section 2.1.3, we have shown thatthe electrical conductivity, σ = ne2τ / m . As the m resistivity is inverse of σ, it can be written as,

The resistivity of materials is

i) inversely proportional to the number density (n) of the electrons

ii) inversely proportional to the average time between the collisions (τ).

In metals, if the temperature increases, the average time between the collision (τ) decreases and n is independent of temperature. In semiconductors when temperature increases, n increases and τ decreases, but increase in n is dominant than decreasing τ, so that overall resistivity decreases.

EXAMPLE 2.13

If the resistance of coil is 3 Ω at 20 0C and α = 0.004/0C then determine its resistance at 100 0C.

Solution

R0= 3 Ω,  T = 100ºC,  T0 = 20ºC

α = 0.004/ºC,  RT = ?

RT= R0(1 + α(T-T0))

R100 = 3(1 + 0.004 × 80)

R100 = 3(1 + 0.32)

R100 = 3(1.32)

R100 = 3.96 Ω

EXAMPLE 2.14

Resistance of a material at 10ºC and 40ºC are 45 Ω and 85 Ω respectively. Find its temperature co-efficient of resistance.

Solution

T0 = 10ºC, T = 40ºC, R0= 45 Ω , R = 85 Ω

 α = 1/R . ΔR /ΔT

α = 0.0296 per ºC