Chapter: 12th Physics : Current Electricity
KirchhoffŌĆÖs Rules: Solved Example Problems
KirchhoffŌĆÖs first rule (Current rule or Junction rule): Solved Example Problems
EXAMPLE 2.20
From the given circuit find the value of I.
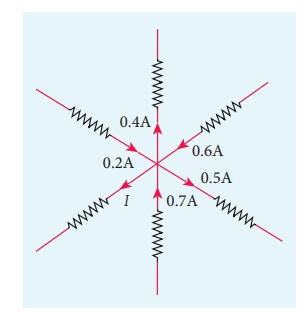
Solution
Applying KirchoffŌĆÖs rule to the point P in the circuit,
The arrows pointing towards P are positive and away from P are negative.
Therefore, 0.2A ŌĆō 0.4A + 0.6A ŌĆō 0.5A + 0.7A ŌĆō I = 0
1.5A ŌĆō 0.9A ŌĆō I = 0
0.6A ŌĆō I = 0
I = 0.6 A
KirchhoffŌĆÖs Second rule (Voltage rule or Loop rule) : Solved Example Problems
EXAMPLE 2.21
The following figure shows a complex network of conductors which can be divided into two closed loops like ACE and ABC. Apply KirchoffŌĆÖs voltage rule.

Solution
Thus applying KirchoffŌĆÖs second law to the closed loop EACE
I1R1 + I2R2 + I3R3 = ╬Š
and for the closed loop ABCA
I4R4 + I5R5-I2R2= 0
EXAMPLE 2.22
Calculate the current that flows in the 1ŌĆå╬® resistor in the following circuit.

Solution

We can denote the current that flows from 9V battery as I1 and it splits into I2 and I1 ŌĆō I2 in the junction according KirchoffŌĆÖs current rule (KCR). It is shown below.
Now consider the loop EFCBE and apply KVR, we get
1I2 + 3I1 + 2I1 = 9
5I1 + I2 = 9 (1)
Applying KVR to the loop EADFE, we get
3 (I1 ŌĆō I2 ) ŌĆō 1I2 = 6
3I1 ŌĆō 4I2 = 6 (2)
Solving equation (1) and (2), we get
I1 = 1.83 A and I2 = -0.13 A
It implies that the current in the 1 ohm resistor flows from F to E.
WheatstoneŌĆÖs bridge : Solved Example Problems
EXAMPLE 2.23
In a WheatstoneŌĆÖs bridge P = 100 ╬®, Q = 1000 ╬® and R = 40 ╬®. If the galvanometer shows zero deflection, determine the value of S.
Solution
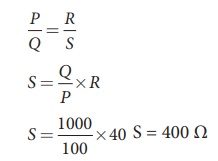
EXAMPLE 2.24
What is the value of x when the WheatstoneŌĆÖs network is balanced?
P = 500 ╬®, Q = 800 ╬®, R = x + 400, S = 1000 ╬®

Solution
P/Q = R/S
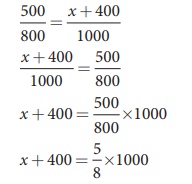
x + 400 = 0.625 ├Ś 1000
x + 400 = 625
x = 625 ŌĆō 400
x = 225 ╬®
Meter bridge : Solved Example Problems
EXAMPLE 2.25
In a meter bridge with a standard resistance of 15 ╬® in the right gap, the ratio of balancing length is 3:2. Find the value of the other resistance.
Solution

EXAMPLE 2.25
In a meter bridge, the value of resistance in the resistance box is 10 ╬®. The balancing length is l1 = 55 cm. Find the value of unknown resistance.
Solution
Q = 10 Ōä”
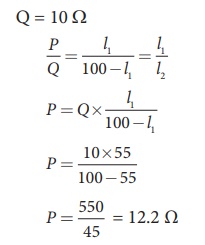
Related Topics