Chapter: 12th Physics : Current Electricity
Electric Current
ELECTRIC CURRENT
Matter is made up of atoms. Each atom consists of a positively charged nucleus with negatively charged electrons moving around the nucleus. Atoms in metals have one or more electrons which are loosely bound to the nucleus. These electrons are called free electrons and can be easily detached from the atoms. The substances which have an abundance of these free electrons are called conductors. These free electrons move at random throughout the conductor at a given temperature. In general due to this random motion, there is no net transfer of charges from one end of the conductor to other end and hence no current.
When a potential difference is
applied by the battery across the ends of the conductor, the free electrons
drift towards the positive terminal of the battery, producing a net electric
current. This is easily understandable from the analogy given in the Figure
2.1.![]()
![]()

In the XI Volume 2, unit 6, we studied, that the mass move from higher gravitational potential to lower gravitational potential. Likewise, positive charge flows from higher electric potential to lower electric potential and negative charge flows from lower electric potential to higher electric potential. So battery or electric cell simply creates potential difference across the conductor.
The electric current in
a conductor is defined as the rate of flow of charges through a given
cross-sectional area A. It is shown in the Figure 2.2.

If a net charge Q passes through any cross section of a conductor
in time t, then the current is defined as I = Q/t . But charge flow is not
always constant. Hence current can more generally be defined as

Where ŌłåQ is the amount
of charge that passes through the conductor at any cross section during the
time interval Ōłåt. If the rate at which charge flows changes in time, the
current also changes. The instantaneous current I is defined as the limit of
the average current, as ╬ö t ŌåÆ 0

The SI unit of current is the ampere (A)
That is, 1A of current
is equivalent to 1 Coulomb of charge passing through a perpendicular cross
section in 1second. The electric current is a scalar quantity.
EXAMPLE 2.1
Compute the current in
the wire if a charge of 120 C is flowing through a copper wire in 1 minute.
Solution
The current (rate of
flow of charge) in the wire is
I = Q/t = 120/60 = 2A
1. Conventional Current
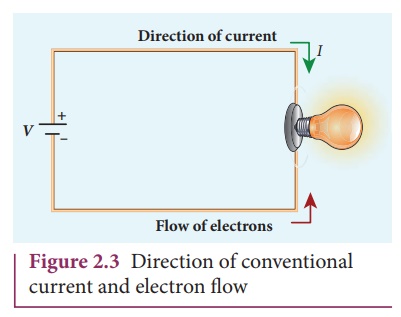
In an electric circuit, arrow heads are used to indicate the direction of flow of current. By convention, this flow in the circuit should be from the positive terminal of the battery to the negative terminal. This current is called the conventional current or simply current and is in the direction in which a positive test charge would move. In typical circuits the charges that flow are actually electrons, from the negative terminal of the battery to the positive. As a result, the flow of electrons and the direction of conventional current points in opposite direction as shown in Figure 2.3. Mathematically, a transfer of positive charge is the same as a transfer of negative charge in the opposite direction.
2. Drift velocity
In a conductor the
charge carriers are free electrons. These electrons move freely through the
conductor and collide repeatedly with the positive ions. If there is no
electric field, the electrons move in random directions, so the directions of
their velocities are also completely random direction. On an average, the
number of electrons travelling in any direction will be equal to the number of
electrons travelling in the opposite direction. As a result, there is no net
flow of electrons in any direction and hence there will not be any current.
Suppose a potential
difference is set across the
conductor by connecting
a battery,
an electric field ![]() is created in the conductor. This electric field
exerts a force on the electrons, producing a current. The electric field
accelerates the electrons, while ions scatter the electrons and change the
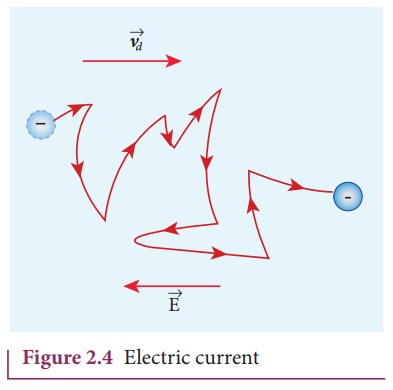
direction of motion. Thus, we have zigzag paths of electrons. In addition to
the zigzag motion due to the collisions, the electrons move slowly along the
conductor in a direction opposite to that of
is created in the conductor. This electric field
exerts a force on the electrons, producing a current. The electric field
accelerates the electrons, while ions scatter the electrons and change the
direction of motion. Thus, we have zigzag paths of electrons. In addition to
the zigzag motion due to the collisions, the electrons move slowly along the
conductor in a direction opposite to that of ![]() as shown in the Figure
2.4.
as shown in the Figure
2.4.
Ions
Any material is made up of neutral atoms with equal number of electrons and protons. If the outermost electrons leave the atoms, they become free electrons and are responsible for electric current. The atoms after losing their outer most electrons will have more positive charges and hence are called positive ions. These ions will not move freely within the material like the free electrons. Hence the positive ions will not give rise to current.
This velocity is called
drift velocity ![]() d . The drift velocity is the average
velocity acquired by the electrons inside the conductor when it is subjected to
an electric field. The average time between successive collisions is called the
mean free time denoted by Žä. The acceleration
d . The drift velocity is the average
velocity acquired by the electrons inside the conductor when it is subjected to
an electric field. The average time between successive collisions is called the
mean free time denoted by Žä. The acceleration ![]() experienced by
the electron in an electric field
experienced by
the electron in an electric field ![]() is given by
is given by
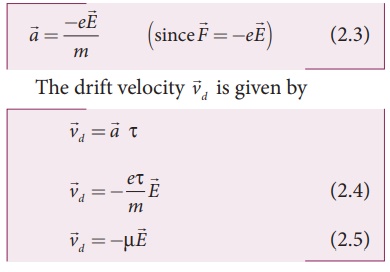
Here ┬Ą = eŽä/m is the mobility
of the electron and it is defined
as the magnitude of the drift velocity per unit electric field.

The SI unit of mobility is m2/Vs.
EXAMPLE 2.2
If an electric field of
magnitude 570 N C-1, is applied in the copper wire, find the
acceleration experienced by the electron.
Solution:
E = 570 N C-1,
e = 1.6 ├Ś 10-19 C, m = 9.11 ├Ś 10-31 kg and a = ?
F = ma = eE
a = eE/m = 570├Ś1 .6├Ś10ŌłÆ19/9 .11├Ś10-31
= 912 ├Ś10ŌłÆ19
├Ś1031 / 9 .11
= 1.001 ├Ś 1014 m s-2
Misconception
(i) There is a common misconception that the
battery is the source of electrons. It is not true. When a battery is connected
across the given wire, the electrons in the closed circuit resulting the
current. Battery sets the potential difference (electrical energy) due to which
these electrons in the conducting wire flow in a particular direction. The
resulting electrical energy is used by electric bulb, electric fan etc.
Similarly the electricity board is supplying the electrical energy to our home.
(ii) We often use the
phrases like ŌĆścharging the battery in my mobileŌĆÖ and ŌĆśmy mobile phone battery
has no chargeŌĆÖ etc. These sentences are not correct.

When we say ŌĆśbattery has
no chargeŌĆÖ, it means, that the battery has lost ability to provide energy or
provide potential difference to the electrons in the circuit. When we say
ŌĆśmobile is chargingŌĆÖ, it implies that the battery is receiving energy from AC
power supply and not electrons.
3. Microscopic model of current
Consider a conductor
with area of cross section A and an electric field ![]() applied
from right to left. Suppose there are n electrons per unit volume in the
conductor and assume that all the electrons move with the same drift velocity
applied
from right to left. Suppose there are n electrons per unit volume in the
conductor and assume that all the electrons move with the same drift velocity ![]() d
as shown in Figure 2.5.
d
as shown in Figure 2.5.

The drift velocity of
the electrons = vd The electrons move through a distance dx
within a small interval of dt
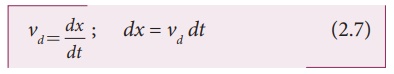
Since A is the area of
cross section of the conductor, the electrons available in the volume of length
dx is = volume ├Ś number per unit volume

Substituting for dx
from equation (2.7) in (2.8)![]()
![]()
= (A vd dt )
n
Total charge in volume
element dQ = (charge) ├Ś (number of electrons in the volume element)
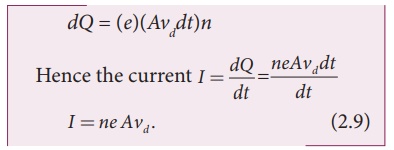
Current density (J)
The current density ( J
) is defined as the current per unit area of cross section of the conductor.
J = I/A
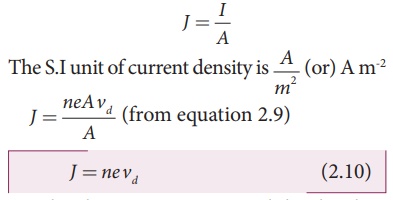
The above expression is
valid only when the direction of the current is perpendicular to the area A. In
general, the current density is a vector quantity and it is given by
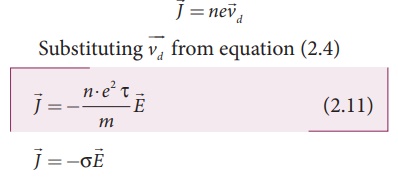
But conventionally, we
take the direction of (conventional) current density as the direction of
electric field. So the above equation becomes

where Žā = ne2Žä /m is called conductivity. The equation 2.12 is called microscopic
form of ohmŌĆÖs law.
The inverse of
conductivity is called resistivity (Žü)
[Refer section 2.2.1].

EXAMPLE 2.3
A copper wire of
cross-sectional area 0.5 mm2 carries a current of 0.2 A. If the free
electron density of copper is 8.4 ├Ś 1028 m-3 then compute
the drift velocity of free electrons.
Solution
The relation between
drift velocity of electrons and current in a wire of cross-sectional area A is
vd = I/ ne A

vd = 0.03 x 10-3 m s-1
EXAMPLE 2.4
Determine the number of
electrons flowing per second through a conductor, when a current of 32 A flows
through it.
Solution
I = 32 A , t = 1 s
Charge of an electron, e
= 1.6 ├Ś 10-19 C
The number of electrons
flowing per second, n =?
I = q/t = ne/t
n = It/e
n = 32├Ś1 / 1 .6├Ś10ŌłÆ19
C
n = 20 ├Ś 1019
= 2 ├Ś 1020 electrons
Related Topics