Kirchhoff’s Second rule (Voltage rule or Loop rule)

Kirchhoff’s Second rule (Voltage rule or Loop rule)

It states that in a closed circuit the algebraic sum of the products of the current and resistance of each part of the circuit is equal to the total emf included in the circuit. This rule follows from the law of conservation of energy for an isolated system (The energy supplied by the emf sources is equal to the sum of the energy delivered to all resistors).The product of current and resistance is taken as positive when the direction of the current is followed. 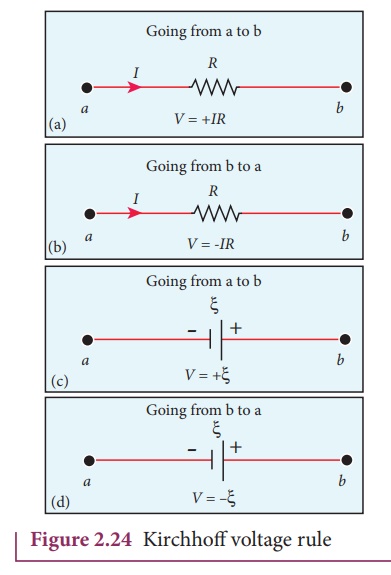Suppose if the direction of current is opposite to the direction of the loop, then product of current and voltage across the resistor is negative. It is shown in Figure 2.24 (a) and (b). The emf is considered positive when proceeding from the negative to the positive terminal of the cell. It is shown in Figure 2.24 (c) and (d).

Kirchhoff voltage rule has to be applied only when all currents in the circuit reach a steady state condition (the current in various branches are constant).

EXAMPLE 2.21

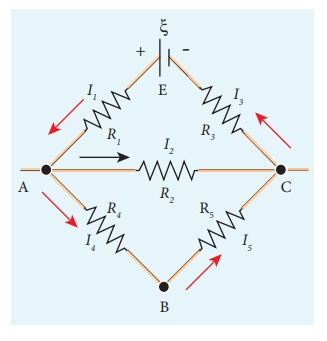
The following figure shows a complex network of conductors which can be divided into two closed loops like ACE and ABC. Apply Kirchoff’s voltage rule.

Solution

Thus applying Kirchoff’s second law to the closed loop EACE 

I₁R₁ + I₂R₂ + I₃R₃ = ξ 

and for the closed loop ABCA

I₄R₄ + I₅R₅-I₂R₂= 0

EXAMPLE 2.22

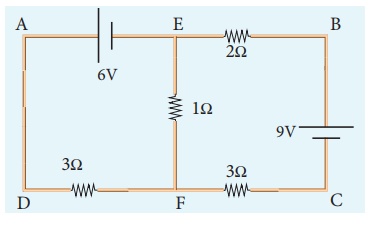
Calculate the current that flows in the 1 Ω resistor in the following circuit.

Solution

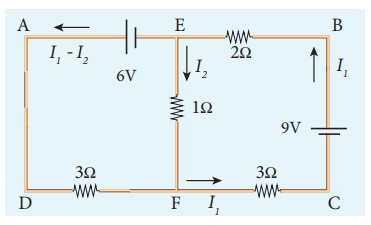
We can denote the current that flows from 9V battery as I₁ and it splits into I₂ and I₁  â€“ I₂ in the junction according Kirchoff’s current rule (KCR). It is shown below.

Now consider the loop EFCBE and apply KVR, we get

1I₂ + 3I₁ + 2I₁ = 9

5I₁ + I₂ = 9 (1)

Applying KVR to the loop EADFE, we get

3 (I₁ – I₂ ) – 1I₂ = 6

3I₁ – 4I₂ = 6 (2)

Solving equation (1) and (2), we get

I₁ = 1.83 A and I₂ = -0.13 A

It implies that the current in the 1 ohm resistor flows from F to E.