Current Electricity - Electric Cells and Batteries | 12th Physics : Current Electricity
Chapter: 12th Physics : Current Electricity
Electric Cells and Batteries
ELECTRIC CELLS AND BATTERIES
An electric cell
converts chemical energy into electrical energy to produce electricity. It
contains two electrodes immersed in an electrolyte as shown in Figure 2.17.
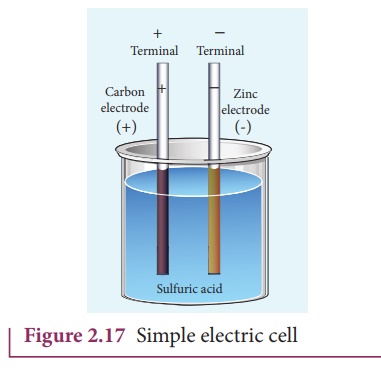
Several electric cells
connected together form a battery. When a cell or battery is connected to a
circuit, electrons flow from the negative terminal to the positive terminal
through the circuit. By using chemical reactions, a battery produces potential
difference across its terminals. This potential difference provides the energy
to move the electrons through the circuit. Commercially available electric
cells and batteries are shown in Figure 2.18


1. Electromotive force and internal resistance
A battery or cell is
called a source of electromotive force (emf). The term ŌĆśelectromotive forceŌĆÖ is
a misnomer since it does not really refer to a force but describes a potential
difference in volts. The emf of a battery or cell is the voltage provided by
the battery when no current flows in the external circuit. It is shown in
Figure 2.19.

Electromotive force
determines the amount of work a battery or cell does to move a certain amount
of charge around the circuit. It is denoted by the symbol ╬Š and to be pronounced as
ŌĆśxiŌĆÖ. An ideal battery has zero internal resistance and the potential
difference (terminal voltage) across the battery equals to its emf. But a real
battery is made of electrodes and electrolyte, there is resistance to the flow
of charges within the battery. This resistance is called internal resistance r.
For a real battery, the terminal voltage is not equal to the emf of the
battery. A freshly prepared cell has low internal resistance and it increases
with ageing.
2. Determination of internal resistance
The circuit connections
are made as shown in Figure 2.20.
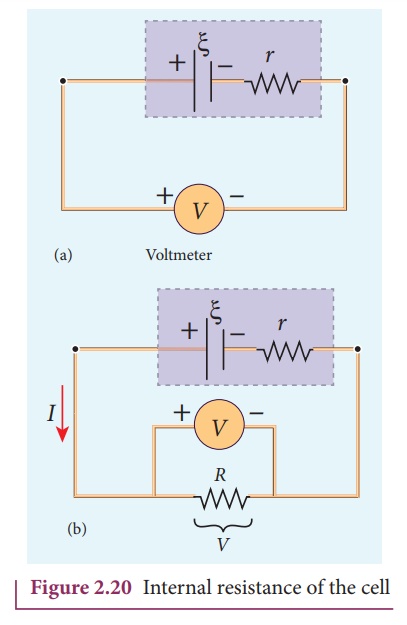
The emf of cell ╬Š is measured by
connecting a high resistance voltmeter across it without connecting the
external resistance R as shown in Figure 2.20(a). Since the voltmeter draws
very little current for deflection, the circuit may be considered as open.
Hence the voltmeter reading gives the emf of the cell. Then, external
resistance R is included in the circuit and current I is established in the
circuit. The potential difference across R is equal to the potential difference
across the cell (V) as shown in Figure 2.20(b).
The potential drop
across the resistor R is

Due to internal
resistance r of the cell, the voltmeter reads a value V, which is less than the
emf of cell ╬Š. It is because, certain
amount of voltage (Ir) has dropped across the internal resistance r.
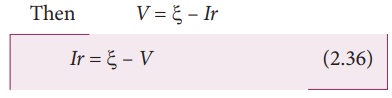
Dividing equation (2.36)
by equation (2.35), we get
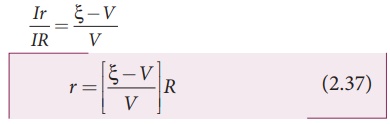
Since ╬Š, V and R
are known, internal resistance r can be determined. We can also find the
total current that flows in the circuit.
Due to this internal
resistance, the power delivered to the circuit is not equal to power rating
mentioned in the battery. For a battery of emf ╬Š, with an internal resistance r, the
power delivered to the circuit of resistance R is given by
P = I╬Š = I (V +
Ir) (from equation 2.36)
Here V is the
voltage drop across the resistance R and it is equal to IR.
Therefore, P = I (IR
+Ir)

Here I2 r is
the power delivered to the internal resistance and I2R is the power
delivered to the electrical device (here it is the resistance R). For a good
battery, the internal resistance r is very small, then I2r
<< I2R and almost entire power is delivered
to the resistance.
EXAMPLE 2.17
A battery has an emf of
12 V and connected to a resistor of 3ŌĆå╬®. The current in the circuit is 3.93ŌĆåA.
Calculate (a) terminal voltage and the internal resistance of the battery (b)
power delivered by the battery and power delivered to the resistor
Solution
The given values I =
3.93 A, ╬Š = 12 V, R = 3 Ōä”
(a) The terminal voltage
of the battery is equal to voltage drop across the resistor
V = IR = 3.93 ├Ś 3 =
11.79 V
The internal resistance
of the battery,
r = |╬Š ŌĆōV / V| R = | 12 ŌłÆ11 .79 /11 .79 | ├Ś 3 = 0.05 ╬®
The power delivered by
the battery P = I╬Š = 3.93 ├Ś 12 = 47.1 W
The power delivered to
the resistor = I2 R = 46.3 W
The remaining power =
(47.1ŌĆåŌĆōŌĆå46.3) P = 0.772 W is delivered to the internal resistance and cannot be
used to do useful work. (it is equal to I2 r).
3. Cells in series
Several cells can be
connected to form a battery. In series connection, the negative terminal of one
cell is connected to the positive terminal of the second cell, the negative
terminal of second cell is connected to the positive terminal of the third cell
and so on. The free positive terminal of the first cell and the free negative
terminal of the last cell become the terminals of the battery.
Suppose n cells, each of
emf ╬Š volts and internal
resistance r ohms are connected in series with an external resistance R
as shown in Figure 2.21
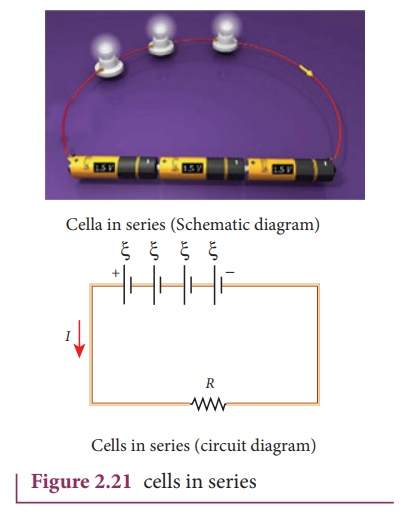
The total emf of the
battery = n╬Š
The total resistance in
the circuit = nr + R By OhmŌĆÖs law, the current in the circuit is

Thus, if r is negligible when compared to R the current supplied by the battery is n times that supplied by a single cell.
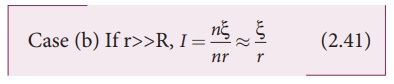
It is the current due to
a single cell. That is, current due to the whole battery is the same as that
due to a single cell and hence there is no advantage in connecting several
cells.
Thus series connection
of cells is advantageous only when the effective internal resistance of the
cells is negligibly small compared with R.

EXAMPLE 2.18
From the given circuit,

Find
i) Equivalent emf of the
combination
ii) Equivalent internal
resistance
iii) Total current
iv) Potential difference
across external resistance
v) Potential difference
across each cell
Solution
i) Equivalent emf of the
combination ╬Šeq = n╬Š = 4 9 = 36 V
ii) Equivalent internal
resistance req = nr = 4 ├Ś 0.1 = 0.4 ╬®
iii) Total current I =
n╬Š / R +nr
= [4 ├Ś9] / 10 + ( 4 ├Ś0.1)
= [4 ├Ś9] / [10 +0 .4] = 36 /10.4
I = 3.46 A
iv) Potential difference
across external resistance V = IR = 3.46 ├Ś 10 = 34.6 V. The remaining 1.4 V is
dropped across the internal resistance of cells.
v) Potential difference
across each cell V/n = 34.6/4 = 8
.65V
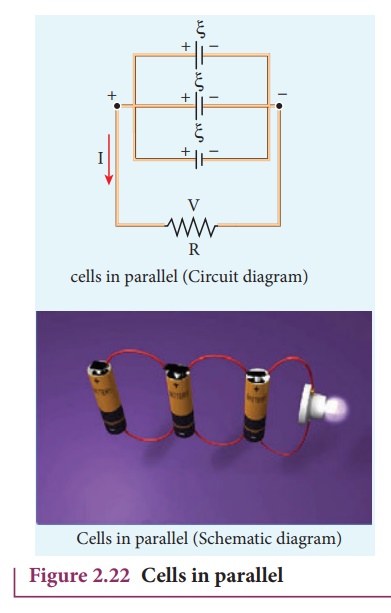
4. Cells in parallel
In parallel connection
all the positive terminals of the cells are connected to one point and all the
negative terminals to a second point. These two points form the positive and
negative terminals of the battery.
Let n cells be connected
in parallel between the points A and B and a resistance R is connected between
the points A and B as shown in Figure 2.22. Let ╬Š be the emf and r the internal resistance of
each cell.
The equivalent internal
resistance of the battery is
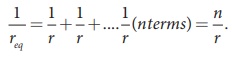
So req = r/n and the total resistance
in the circuit = R +
r/n . The total emf is the potential difference
between the points A and B, which is equal to ╬Š. The current in the circuit is given by![]()
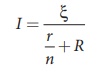
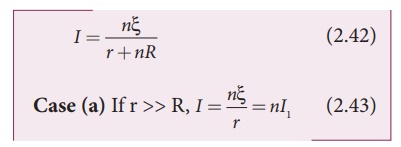
where I1 is
the current due to a single cell and is equal to ╬Š/r when R is negligible.
Thus, the current through the external resistance due to the whole battery is n
times the current due to a single cell.
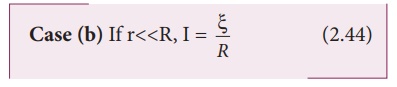
The above equation
implies that current due to the whole battery is the same as that due to a
single cell. Hence it is advantageous to connect cells in parallel when the
external resistance is very small compared to the internal resistance of the
cells.
EXAMPLE 2.19
From the given circuit
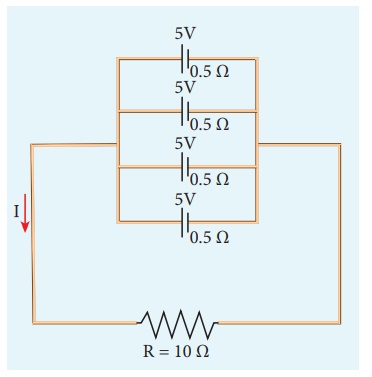
Find
i) Equivalent emf
ii) Equivalent internal
resistance
iii) Total current (I)
iv) Potential difference
across each cell
v) Current from each
cell
Solution
i) Equivalent emf ╬Šeq
= 5 V
ii) Equivalent internal
resistance,
Req = r/n = 0
.5/4 = 0.125╬®
iii) total current,
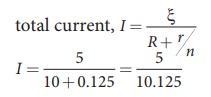
I Ōēł 0.5 A
iv) Potential difference
across each cell V = IR = 0.5 ├Ś 10 = 5 V
v) Current from each
cell, I ŌĆ▓ = I/n
I ŌĆ▓ = 0.5/4 = 0.125 A
Related Topics