Resistivity

Resistivity

In the previous section, we have seen that the resistance R of any conductor is given by

where σ is called the conductivity of the material and it depends only on the type of the material used and not on its dimension.

The resistivity of a material is equal to the reciprocal of its conductivity.

Now we can rewrite equation (2.18) using equation (2.19)

The resistance of a material is directly proportional to the length of the conductor and inversely proportional to the area of cross section of the conductor. The proportionality constant ρ is called the resistivity of the material.

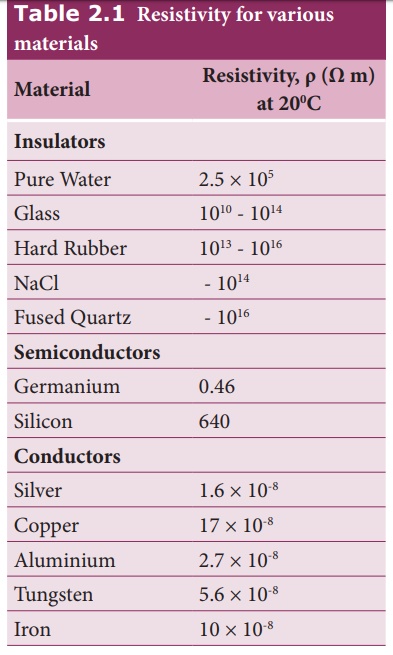
If l = 1 m and A = 1 m2, then the resistance R = ρ. In other words, the electrical resistivity of a material is defined as the resistance offered to current flow by a conductor of unit length having unit area of cross section. The SI unit of ρ is ohm-metre (Ω m). Based on the resistivity, materials are classified as conductors, insulators and semi-conductors. The conductors have lowest resistivity, insulators have highest resistivity and semiconductors have resistivity greater than conductors but less than insulators. The typical resistivity values of some conductors, insulators and semiconductors are given in the Table 2.1

EXAMPLE 2.6

The resistance of a wire is 20 Ω. What will be new resistance, if it is stretched uniformly 8 times its original length?

Solution

R1 = 20 Ω, R2= ?

Let the original length (l1) be l.

The new length, l2 = 8l1 (i.,e) l2 =8l

The original resistance, R = ρ [ l1 / A1]

The new resistance

R2 =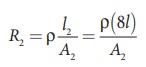 

Though the wire is stretched, its volume is unchanged.

Initial volume = Final volume

A1l1= A2l2 , A1l = A28l

A1 / A2 = 8l / l = 8

By dividing equation R2 by equation R1, we get

Substituting the value of A1/A2, we get

R2 / R1  = 8 ×8 = 64 2

R2 = 64 × 20=1280 Ω

Hence, stretching the length of the wire has increased its resistance.

EXAMPLE 2.7

Consider a rectangular block of metal of height A, width B and length C as shown in the figure.

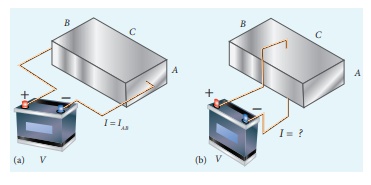
If a potential difference of V is applied between the two faces A and B of the block (figure (a)), the current IAB is observed. Find the current that flows if the same potential difference V is applied between the two faces B and C of the block (figure (b)). Give your answers in terms of IAB.

Solution

In the first case, the resistance of the block