Titrations Based on Acid–Base Reactions: Characterization Applications

Characterization Applications

Two useful characterization applications involving acid–base titrimetry are the determination of equivalent weight, and the determination of acid–base dissociation constants.

Equivalent Weights 

Acid–base titrations can be used to characterize the chemical and physical properties of matter. One simple example is the determination of the equivalent weight* of acids and bases. In this method, an accurately weighed sample of a pure acid or base is titrated to a well-defined equivalence point using a monoprotic strong acid or strong base. If we assume that the titration involves the transfer of n protons, then the moles of titrant needed to reach the equivalence point is given as

Moles titrant = n x moles analyte

and the formula weight is

Since the actual number of protons transferred between the analyte and titrant is uncertain, we define the analyte’s equivalent weight (EW) as the apparent formula weight when n = 1. The true formula weight, therefore, is an integer multiple of the calculated equivalent weight.

FW = n x EW

Thus, if we titrate a monoprotic weak acid with a strong base, the EW and FW are identical. If the weak acid is diprotic, however, and we titrate to its second equivalence point, the FW will be twice as large as the EW.

Equilibrium Constants 

Another application of acid–base titrimetry is the determi- nation of equilibrium constants. Consider, for example, the titration of a weak acid, HA, with a strong base. The dissociation constant for the weak acid is

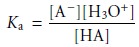
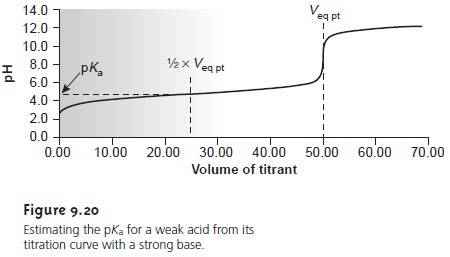
When the concentrations of HA and A– are equal, equation 9.9 reduces to K_a = [H₃O+], or pH = pK_a. Thus, the pK_a for a weak acid can be determined by measuring the pH for a solution in which half of the weak acid has been neutralized. On a titration curve, the point of half-neutralization is approximated by the volume of titrant that is half of that needed to reach the equivalence point. As shown in Figure 9.20, an estimate of the weak acid’s pK_a can be obtained directly from the titra- tion curve.

This method provides a reasonable estimate of the pK_a, provided that the weak acid is neither too strong nor too weak. These limitations are easily appreciated by considering two limiting cases. For the first case let’s assume that the acid is strong enough that it is more than 50% dissociated before the titration begins. As a result the concentration of HA before the equivalence point is always less than the con- centration of A–, and there is no point along the titration curve where [HA] = [A–]. At the other extreme, if the acid is too weak, the equilibrium constant for the titra- tion reaction

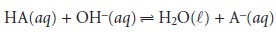
may be so small that less than 50% of HA will have reacted at the equivalence point. In this case the concentration of HA before the equivalence point is always greater than that of A–. 

Determining the pK_a by the half-equivalence point method overes- timates its value if the acid is too strong and underestimates its value if the acid is too weak.

A second approach for determining the pK_a of an acid is to replot the titration curve in a linear form as a Gran plot. For example, earlier we learned that the titra- tion of a weak acid with a strong base can be plotted in a linear form using the fol- lowing equation

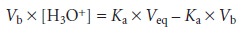
Plotting V_b x [H₃O+] versus V_b, for volumes less than the equivalence point volume yields a straight line with a slope of –K_a. Other linearizations have been developed that use all the points on a titration curve or require no assumptions. This ap- proach to determining acidity constants has been used to study the acid–base prop- erties of humic acids, which are naturally occurring, large-molecular-weight organic acids with multiple acidic sites. In one study, a sample of humic acid was found to have six titratable sites, three of which were identified as carboxylic acids, two of which were believed to be secondary or tertiary amines, and one of which was iden- tified as a phenolic group.