Selecting and Evaluating the End Point - Titrations Based on Acid–Base Reactions

Selecting and Evaluating the End Point

Earlier we made an important distinction between an end point and an equivalence point. The difference between these two terms is important and deserves repeating. The equivalence point occurs when stoichiometrically equal amounts of analyte and titrant react. For example, if the analyte is a triprotic weak acid, a titration with NaOH will have three equivalence points corresponding to the addition of one, two, and three moles of OH– for each mole of the weak acid. An equivalence point, therefore, is a theoretical not an experimental value.

An end point for a titration is determined experimentally and represents the analyst’s best estimate of the corresponding equivalence point. Any difference be- tween an equivalence point and its end point is a source of determinate error. As we shall see, it is even possible that an equivalence point will not have an associated end point.

Where Is the Equivalence Point? 

We have already learned how to calculate the equivalence point for the titration of a strong acid with a strong base, and for the titration of a weak acid with a strong base. We also have learned to sketch a titra- tion curve with a minimum of calculations. Can we also locate the equivalence point without performing any calculations? The answer, as you may have guessed, is often yes!

It has been shown3 that for most acid–base titrations the inflection point, which corresponds to the greatest slope in the titration curve, very nearly coincides with the equivalence point. The inflection point actually precedes the equivalence point, with the error approaching 0.1% for weak acids or weak bases with dissocia- tion constants smaller than 10–9, or for very dilute solutions. Equivalence points de- termined in this fashion are indicated on the titration curves in Figure 9.8.

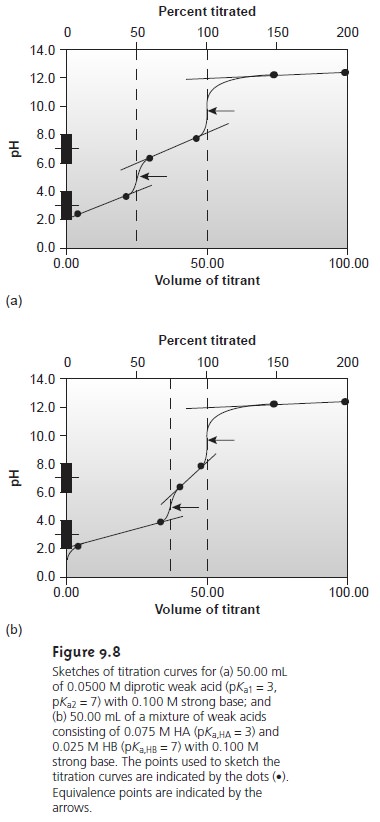
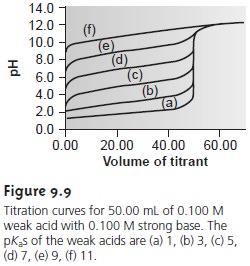
The principal limitation to using a titration curve to locate the equivalence point is that an inflection point must be present. Sometimes, however, an inflection point may be missing or difficult to detect. Figure 9.9, for example, demonstrates the influence of the acid dissociation constant, K_a, on the titration curve for a weak acid with a strong base titrant. The inflection point is visible, even if barely so, for acid dissociation constants larger than 10–9, but is missing when K_a is 10–11.

Another situation in which an inflection point may be missing or difficult to detect occurs when the analyte is a multiprotic weak acid or base whose successive dissociation constants are similar in magnitude. To see why this is true let’s con- sider the titration of a diprotic weak acid, H₂A, with NaOH. During the titration the following two reactions occur.

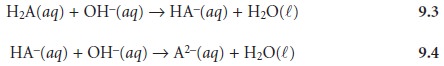
Two distinct inflection points are seen if reaction 9.3 is essentially complete before reaction 9.4 begins.

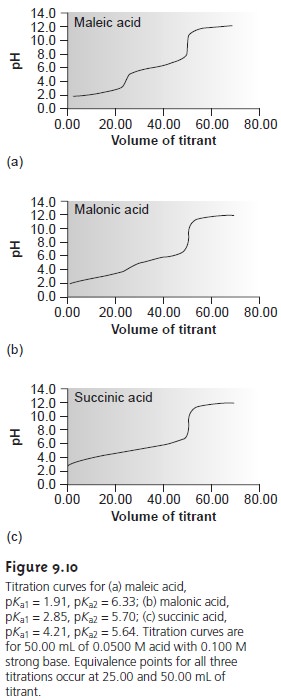
Figure 9.10 shows titration curves for three diprotic weak acids. The titra- tion curve for maleic acid, for which K_a1 is approximately 20,000 times larger than K_a2, shows two very distinct inflection points. Malonic acid, on the other hand, has acid dissociation constants that differ by a factor of approximately 690. Although malonic acid’s titration curve shows two inflection points, the first is not as distinct as that for maleic acid. Finally, the titration curve for suc- cinic acid, for which the two K_a values differ by a factor of only 27, has only a single inflection point corresponding to the neutralization of HC₄H₄O₄– to C₄H O 2–. In general, separate inflection points are seen when successive acid dissociation constants differ by a factor of at least 500 (a ∆pK_a of at least 2.7).

Finding the End Point with a Visual Indicator 

One interesting group of weak acids and bases are derivatives of organic dyes. Because such com- pounds have at least one conjugate acid–base species that is highly colored, their titration results in a change in both pH and color. This change in color can serve as a useful means for determining the end point of a titration, pro- vided that it occurs at the titration’s equivalence point.

The pH at which an acid–base indicator changes color is determined by its acid dissociation constant. For an indicator that is a monoprotic weak acid, HIn, the following dissociation reaction occurs

HIn(aq)+ H₂O(l)  < == == >  H₃O+(aq)+ In–(aq)

for which the equilibrium constant is

                   9.5

Taking the negative log of each side of equation 9.5, and rearranging to solve for pH gives a familiar equation.

                  9.6

The two forms of the indicator, HIn and In–, have different colors. The color of a solution containing an indicator, therefore, continuously changes as the concen- tration of HIn decreases and the concentration of In– increases. If we assume that both HIn and In– can be detected with equal ease, then the transition between the two colors reaches its midpoint when their concentrations are identical or when the pH is equal to the indicator’s pK_a. The equivalence point and the end point coin- cide, therefore, if an indicator is selected whose pK_a is equal to the pH at the equiva- lence point, and the titration is continued until the indicator’s color is exactly halfway between that for HIn and In–. Unfortunately, the exact pH at the equiva- lence point is rarely known. In addition, detecting the point where the concentra- tions of HIn and In– are equal may be difficult if the change in color is subtle.

We can establish a range of pHs over which the average analyst will observe a change in color if we assume that a solution of the indicator is the color of HIn whenever its concentration is ten times more than that of In–, and the color of In– whenever the concentration of HIn is ten times less than that of In–. 

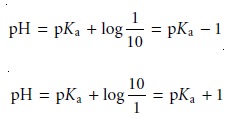
Substi- tuting these inequalities into equation 9.6 shows that an indicator changes color over a pH range of ±1 units on either side of its pK_a (Figure 9.11). Thus, the indicator will be the color of HIn when the pH is less than pK_a – 1, and the color of In– for pHs greater than pK_a + 1.

The pH range of an indicator does not have to be equally distributed on either side of the indicator’s pK_a. For some indicators only the weak acid or weak base is col- ored. For other indicators both the weak acid and weak base are colored, but one form may be easier to see. In either case, the pH range is skewed toward those pH lev- els for which the less colored form of the indicator is present in higher concentration.

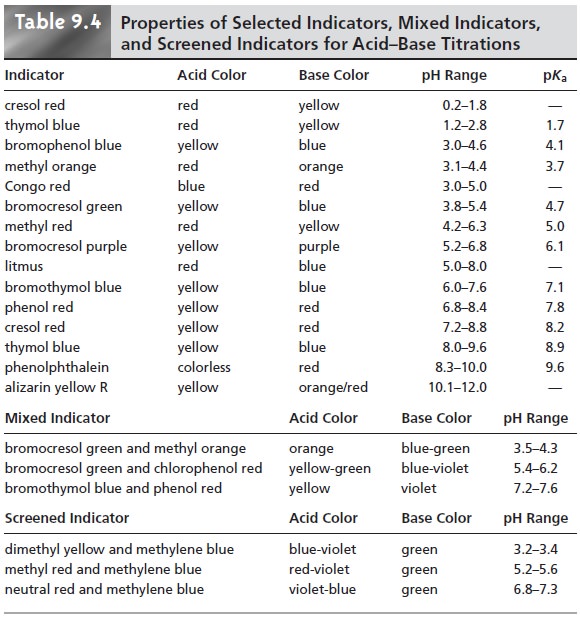
A list of several common acid–base indicators, along with their pK_as, color changes, and pH ranges, is provided in the top portion of Table 9.4. 

In some cases, mixed indicators, which are a mixture of two or more acid–base indicators, provide a narrower range of pHs over which the color change occurs. A few examples of such mixed indicators are included in the middle portion of Table 9.4. Adding a neutral screening dye, such as methylene blue, also has been found to narrow the pH range over which an indicator changes color (lower portion of Table 9.4). In this case, the neutral dye provides a gray color at the midpoint of the indicator’s color transition.

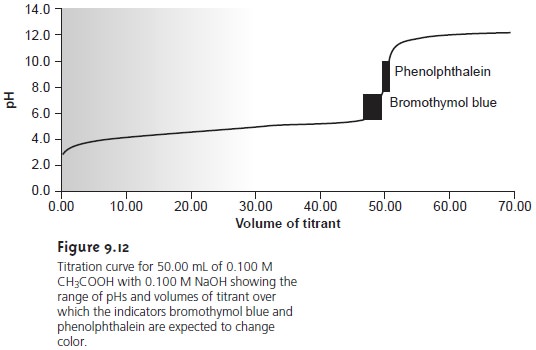
The relatively broad range of pHs over which any indicator changes color places additional limitations on the feasibility of a titration. To minimize a determi- nate titration error, an indicator’s entire color transition must lie within the sharp transition in pH occurring near the equivalence point. Thus, in Figure 9.12 we see that phenolphthalein is an appropriate indicator for the titration of 0.1 M acetic acid with 0.1 M NaOH. Bromothymol blue, on the other hand, is an inappropriate indicator since its change in color begins before the initial sharp rise in pH and, as a result, spans a relatively large range of volumes. The early change in color increases the probability of obtaining inaccurate results, and the range of possible end point volumes increases the probability of obtaining imprecise results.

The need for the indicator’s color transition to occur in the sharply rising por- tion of the titration curve justifies our earlier statement that not every equivalence point has an end point. For example, trying to use a visual indicator to find the first equivalence point in the titration of succinic acid (see Figure 9.10c) is pointless since any difference between the equivalence point and the end point leads to a large titration error.

Finding the End Point by Monitoring pH 

An alternative approach to finding a titration’s end point is to monitor the titration reaction with a suitable sensor whose signal changes as a function of the analyte’s concentration. Plotting the data gives us the resulting titration curve. The end point may then be determined from the titration curve with only a minimal error.

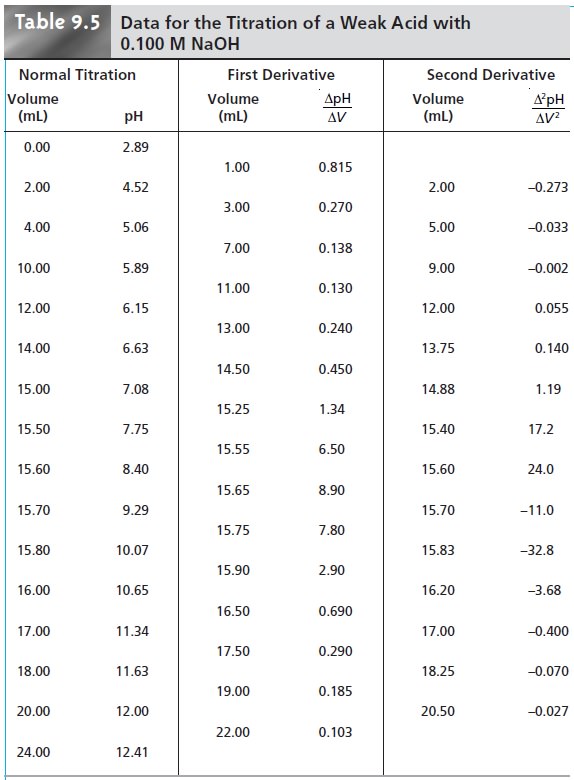
The most obvious sensor for an acid–base titration is a pH electrode.* For ex- ample, Table 9.5 lists values for the pH and volume of titrant obtained during the titration of a weak acid with NaOH. The resulting titration curve, which is called a potentiometric titration curve, is shown in Figure 9.13a. The simplest method for finding the end point is to visually locate the inflection point of the titration curve. This is also the least accurate method, particularly if the titration curve’s slope at the equivalence point is small.

The second derivative of a titration curve may be more useful than the first de- rivative, since the end point is indicated by its intersection with the volume axis. The second derivative is approximated as ∆(∆pH/∆V)/∆V, or ∆2pH/∆V 2. For the titration data in Table 9.5, the initial point in the second derivative titration curve is

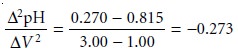
and is plotted as the average of the two volumes (2.00 mL). The remainder of the data for the second derivative titration curve are shown in Table 9.5 and plotted in Figure 9.13c.

Derivative methods are particularly well suited for locating end points in multi- protic and multicomponent systems, in which the use of separate visual indicators for each end point is impractical. The precision with which the end point may be located also makes derivative methods attractive for the analysis of samples with poorly defined normal titration curves.

Derivative methods work well only when sufficient data are recorded during the sharp rise in pH occurring near the equivalence point. This is usually not a problem when the titration is conducted with an automatic titrator, particularly when operated under computer control. Manual titrations, however, often contain only a few data points in the equivalence point region, due to the limited range of volumes over which the transition in pH occurs. Manual titrations are, however, information-rich during the more gently rising portions of the titration curve be- fore and after the equivalence point.

Consider again the titration of a monoprotic weak acid, HA, with a strong base. At any point during the titration the weak acid is in equilibrium with H₃O+ and A–

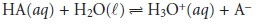
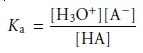
Before the equivalence point, and for volumes of titrant in the titration curve’s buffer region, the concentrations of HA and A– are given by the following equations.

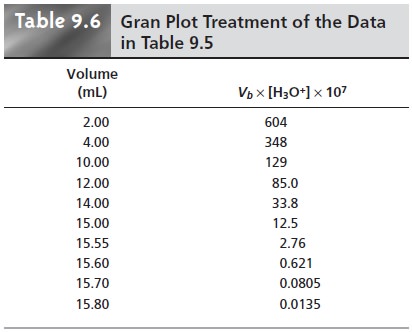
For volumes of titrant before the equivalence point, a plot of V_b x [H₃O+] versus V_b is a straight line with an x-intercept equal to the volume of titrant at the end point and a slope equal to –K_a.* Results for the data in Table 9.5 are shown in Table 9.6 and plotted in Figure 9.13d. Plots such as this, which convert a portion of a titration curve into a straight line, are called Gran plots.

Finding the End Point by Monitoring Temperature 

The reaction between an acid and a base is exothermic. Heat generated by the reaction increases the temperature of the titration mixture. The progress of the titration, therefore, can be followed by monitoring the change in temperature.

An idealized thermometric titration curve (Figure 9.14a) consists of three distinct linear regions. Before adding titrant, any change in temperature is due to the cooling or warming of the solution containing the analyte. Adding titrant ini- tiates the exothermic acid–base reaction, resulting in an increase in temperature. This part of a thermometric titration curve is called the titration branch.

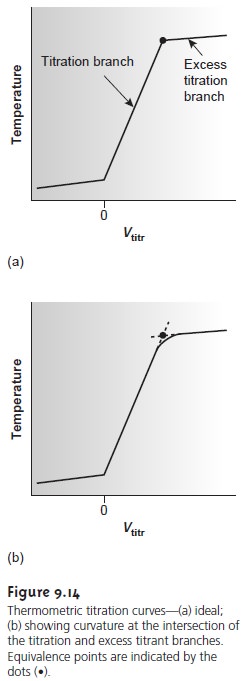
The temperature continues to rise with each addition of titrant until the equivalence point is reached. After the equivalence point, any change in temperature is due to the difference between the temperatures of the analytical solution and the titrant, and the enthalpy of dilution for the excess titrant. Actual thermometric titration curves (Figure 9.14b) frequently show curvature at the intersection of the titration branch and the excess titrant branch due to the incompleteness of the neutraliza- tion reaction, or excessive dilution of the analyte during the titration. The latter problem is minimized by using a titrant that is 10–100 times more concentrated than the analyte, although this results in a very small end point volume and a larger relative error.

The end point is indicated by the intersection of the titration branch and the excess titrant branch. In the idealized thermometric titration curve (see Figure 9.14a) the end point is easily located. When the intersection between the two branches is curved, the end point can be found by extrapolation (Figure 9.14b).

Although not commonly used, thermometric titrations have one distinct ad- vantage over methods based on the direct or indirect monitoring of pH. As dis- cussed earlier, visual indicators and potentiometric titration curves are limited by the magnitude of the relevant equilibrium constants. For example, the titra- tion of boric acid, H₃BO₃, for which K_a is 5.8 x 10–10, yields a poorly defined equivalence point (Figure 9.15a). The enthalpy of neutralization for boric acid with NaOH, however, is only 23% less than that for a strong acid (–42.7 kJ/mol for H₃BO₃ versus –55.6 kJ/mol for HCl), resulting in a favorable thermometric titration curve (Figure 9.15b).