Acid–Base Titration Curves

Acid–Base Titration Curves

In the overview we noted that the experimentally determined end point should coincide with the titration’s equivalence point. For an acid–base titra- tion, the equivalence point is characterized by a pH level that is a function of the acid–base strengths and concentrations of the analyte and titrant. The pH at the end point, however, may or may not correspond to the pH at the equivalence point. To understand the relationship between end points and equivalence points we must know how the pH changes during a titration. In this section we will learn how to construct titration curves for several important types of acid–base titrations.

Titrating Strong Acids and Strong Bases 

For our first titration curve let’s consider the titration of 50.0 mL of 0.100 M HCl with 0.200 M NaOH. For the reaction of a strong base with a strong acid the only equilibrium reaction of importance is

H₃O+(aq)+ OH–(aq) < = = > 2H₂O(l)              9.1

The first task in constructing the titration curve is to calculate the volume of NaOH needed to reach the equivalence point. At the equivalence point we know from re- action 9.1 that

Moles HCl = moles NaOH

or

MaVa = MbVb

where the subscript ‘a’ indicates the acid, HCl, and the subscript ‘b’ indicates the base, NaOH. The volume of NaOH needed to reach the equivalence point, there- fore, is

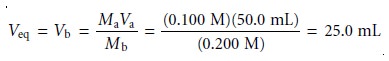
Before the equivalence point, HCl is present in excess and the pH is determined by the concentration of excess HCl. Initially the solution is 0.100 M in HCl, which, since HCl is a strong acid, means that the pH is

pH = –log[H3O⁺] = –log[HCl] = –log(0.100) = 1.00

The equilibrium constant for reaction 9.1 is (K_w)–1, or 1.00 x 1014. Since this is such a large value we can treat reaction 9.1 as though it goes to completion. After adding 10.0 mL of NaOH, therefore, the concentration of excess HCl is

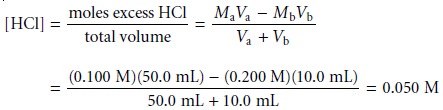
giving a pH of 1.30.

At the equivalence point the moles of HCl and the moles of NaOH are equal. Since neither the acid nor the base is in excess, the pH is determined by the dissoci- ation of water.

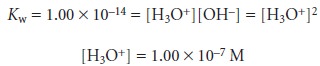
Thus, the pH at the equivalence point is 7.00.

Finally, for volumes of NaOH greater than the equivalence point volume, the pH is determined by the concentration of excess OH–. For example, after adding 30.0 mL of titrant the concentration of OH– is

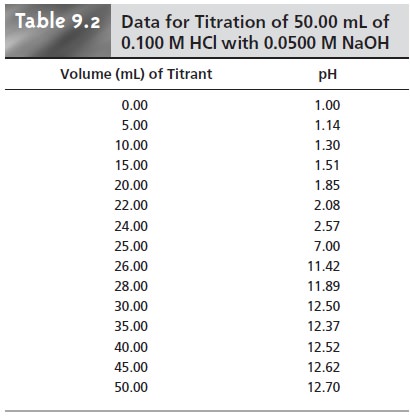
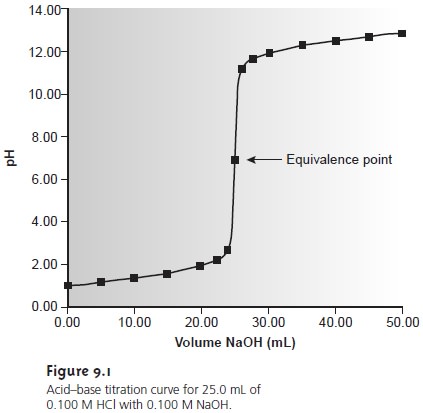
giving a pH of 12.10. Table 9.2 and Figure 9.1 show additional results for this titra- tion curve. Calculating the titration curve for the titration of a strong base with a strong acid is handled in the same manner, except that the strong base is in excess before the equivalence point and the strong acid is in excess after the equivalence point.

Titrating a Weak Acid with a Strong Base 

For this example let’s consider the titra- tion of 50.0 mL of 0.100 M acetic acid, CH₃COOH, with 0.100 M NaOH. Again, we start by calculating the volume of NaOH needed to reach the equivalence point; thus

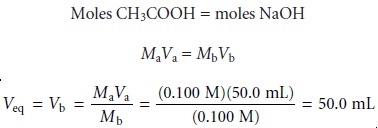
Before adding any NaOH the pH is that for a solution of 0.100 M acetic acid.

At the beginning of the titration the pH is 2.88.

Adding NaOH converts a portion of the acetic acid to its conjugate base.

Any solution containing comparable amounts of a weak acid, HA, and its conjugate weak base, A–, is a buffer. As we learned, we can calculate the pH of a buffer using the Henderson–Hasselbalch equation.

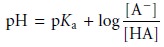
The equilibrium constant for reaction 9.2 is large (K = K_a/K_w = 1.75 x 109), so we can treat the reaction as one that goes to completion. Before the equivalence point, the concentration of unreacted acetic acid is

A similar calculation shows that the pH after adding 20.0 mL of NaOH is 4.58.

At the equivalence point, the moles of acetic acid initially present and the moles of NaOH added are identical. Since their reaction effectively proceeds to completion, the predominate ion in solution is CH₃COO–, which is a weak base. To calcu- late the pH we first determine the concentration of CH₃COO–.

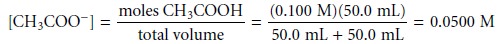
The concentration of H₃O+, therefore, is 1.87 x 10–9, or a pH of 8.73.

After the equivalence point NaOH is present in excess, and the pH is deter- mined in the same manner as in the titration of a strong acid with a strong base. For example, after adding 60.0 mL of NaOH, the concentration of OH– is

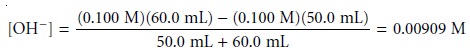
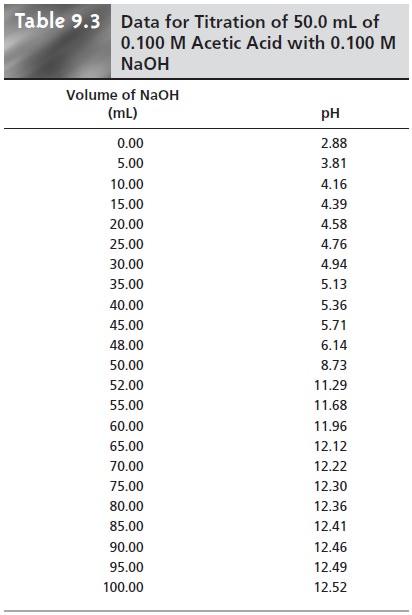
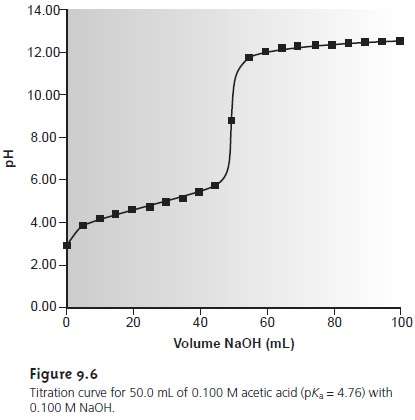
giving a pH of 11.96. Table 9.3 and Figure 9.6 show additional results for this titra- tion. The calculations for the titration of a weak base with a strong acid are handled in a similar manner except that the initial pH is determined by the weak base, the pH at the equivalence point by its conjugate weak acid, and the pH after the equiva- lence point by the concentration of excess strong acid.

The approach that we have worked out for the titration of a monoprotic weak acid with a strong base can be extended to reactions involving multiprotic acids or bases and mixtures of acids or bases. As the complexity of the titration increases, however, the necessary calculations become more time-consuming. Not surpris- ingly, a variety of algebraic1 and computer spreadsheet approaches have been de- scribed to aid in constructing titration curves.

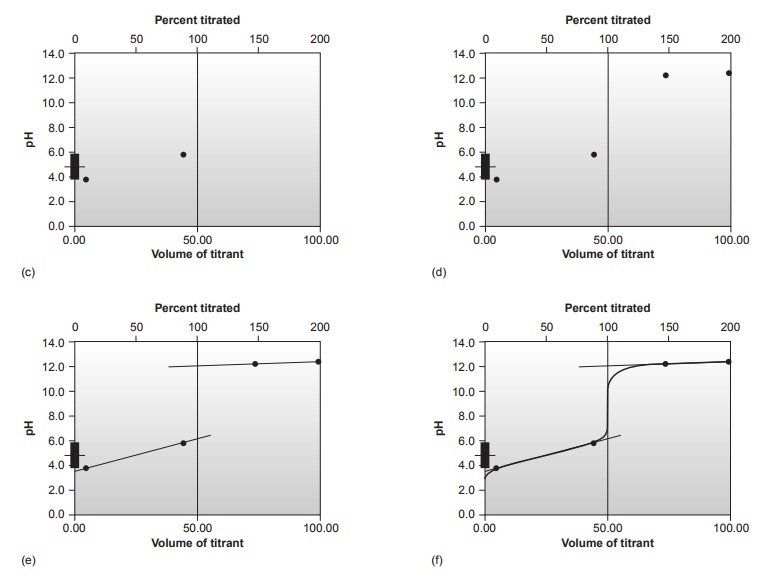
Sketching an Acid–Base Titration Curve 

To evaluate the relationship between an equivalence point and an end point, we only need to construct a reasonable approx- imation to the titration curve. In this section we demonstrate a simple method for sketching any acid–base titration curve. Our goal is to sketch the titration curve quickly, using as few calculations as possible.

To quickly sketch a titration curve we take advantage of the following observa- tion. Except for the initial pH and the pH at the equivalence point, the pH at any point of a titration curve is determined by either an excess of strong acid or strong base, or by a buffer consisting of a weak acid and its conjugate weak base. As we have seen in the preceding sections, calculating the pH of a solution containing ex- cess strong acid or strong base is straightforward.

We can easily calculate the pH of a buffer using the Henderson–Hasselbalch equa- tion. We can avoid this calculation, however, if we make the following assumption. You may recall that we stated that a buffer operates over a pH range ex- tending approximately ±1 pH units on either side of the buffer’s pK_a. The pH is at the lower end of this range, pH = pK_a – 1, when the weak acid’s concentration is approxi- mately ten times greater than that of its conjugate weak base. Conversely, the buffer’s pH is at its upper limit, pH = pK_a + 1, when the concentration of weak acid is ten times less than that of its conjugate weak base. When titrating a weak acid or weak base, therefore, the buffer region spans a range of volumes from approximately 10% of the equivalence point volume to approximately 90% of the equivalence point volume.*

Our strategy for quickly sketching a titration curve is simple. We begin by draw- ing our axes, placing pH on the y-axis and volume of titrant on the x-axis. After calcu- lating the volume of titrant needed to reach the equivalence point, we draw a vertical line that intersects the x-axis at this volume. Next, we determine the pH for two vol- umes before the equivalence point and for two volumes after the equivalence point. To save time we only calculate pH values when the pH is determined by excess strong acid or strong base. For weak acids or bases we use the limits of their buffer region to esti- mate the two points. Straight lines are drawn through each pair of points, with each line intersecting the vertical line representing the equivalence point volume. Finally, a smooth curve is drawn connecting the three straight-line segments. Example 9.1 illus- trates this approach for the titration of a weak acid with a strong base.

This approach can be used to sketch titration curves for other acid–base titra- tions including those involving polyprotic weak acids and bases or mixtures of weak acids and bases (Figure 9.8). Figure 9.8a, for example, shows the titration curve when titrating a diprotic weak acid, H₂A, with a strong base. 

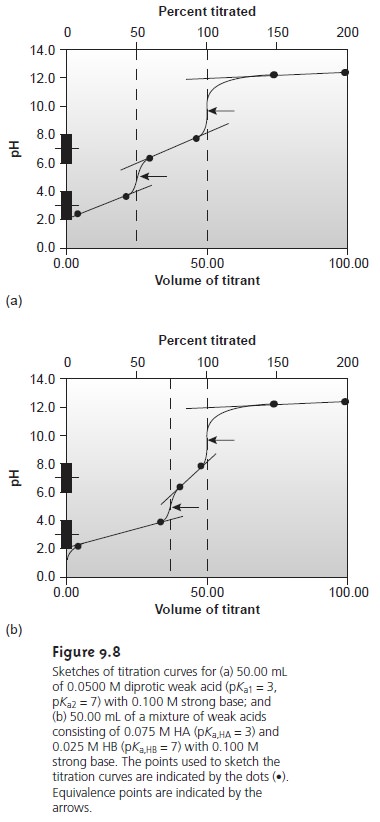
Since the analyte is diprotic there are two equivalence points, each requiring the same volume of titrant. Before the first equivalence point the pH is controlled by a buffer consisting of H₂A and HA–, and the HA–/A2– buffer determines the pH between the two equiv- alence points. After the second equivalence point, the pH reflects the concentration of the excess strong base titrant.

Figure 9.8b shows a titration curve for a mixture consisting of two weak acids: HA and HB. Again, there are two equivalence points. In this case, however, the equivalence points do not require the same volume of titrant because the concen- tration of HA is greater than that for HB. Since HA is the stronger of the two weak acids, it reacts first; thus, the pH before the first equivalence point is controlled by the HA/A– buffer. Between the two equivalence points the pH reflects the titration of HB and is determined by the HB/B– buffer. Finally, after the second equivalence point, the excess strong base titrant is responsible for the pH.