Redox Titration Curves

Redox Titration Curves

To evaluate a redox titration we must know the shape of its titration curve. In an acid–base titration or a complexation titration, a titration curve shows the change in concentration of H₃O+ (as pH) or Mn+ (as pM) as a function of the volume of titrant. For a redox titration, it is convenient to monitor electrochemical potential.

You will recall that the Nernst equation relates the electro- chemical potential to the concentrations of reactants and products participating in a redox reaction. Consider, for example, a titration in which the analyte in a reduced state, A_red, is titrated with a titrant in an oxidized state, T_ox. The titration reaction is

Ared + Tox < == == >  Tred + Aox

The electrochemical potential for the reaction is the difference between the reduc- tion potentials for the reduction and oxidation half-reactions; thus,

Erxn = ETox/Tred – EAox/Ared

After each addition of titrant, the reaction between the analyte and titrant reaches a state of equilibrium. The reaction’s electrochemical potential, E_rxn, therefore, is zero, and

ETox/Tred = EAox /Ared

Consequently, the potential for either half-reaction may be used to monitor the titration’s progress.

Before the equivalence point the titration mixture consists of appreciable quan- tities of both the oxidized and reduced forms of the analyte, but very little unreacted titrant. The potential, therefore, is best calculated using the Nernst equation for the analyte’s half-reaction

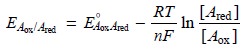
Although E˚_Aox /Ared is the standard-state potential for the analyte’s half-reaction, a matrix-dependent formal potential is used in its place. After the equivalence point, the potential is easiest to calculate using the Nernst equation for the titrant’s half-reaction, since significant quantities of its oxidized and reduced forms are present.

Calculating the Titration Curve 

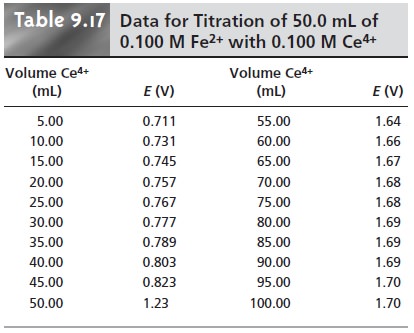
As an example, let’s calculate the titration curve for the titration of 50.0 mL of 0.100 M Fe2+ with 0.100 M Ce4+ in a matrix of 1 M HClO₄. The reaction in this case is

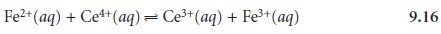
The equilibrium constant for this reaction is quite large (it is approximately 6 x 1015), so we may assume that the analyte and titrant react completely.

The first task is to calculate the volume of Ce4+ needed to reach the equivalence point. From the stoichiometry of the reaction we know

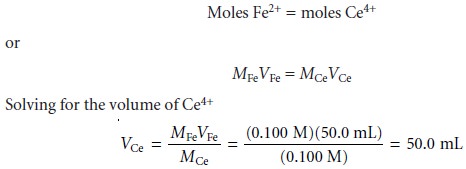
gives the equivalence point volume as 50.0 mL.

Before the equivalence point the concentration of unreacted Fe2+ and the con- centration of Fe3+ produced by reaction 9.16 are easy to calculate. For this reason we find the potential using the Nernst equation for the analyte’s half-reaction

At the equivalence point, the moles of Fe2+ initially present and the moles of Ce4+ added are equal. Because the equilibrium constant for reaction 9.16 is large, the concentrations of Fe2+ and Ce4+ are exceedingly small and difficult to calculate without resorting to a complex equilibrium problem. Consequently, we cannot cal- culate the potential at the equivalence point, E_eq, using just the Nernst equation for the analyte’s half-reaction or the titrant’s half-reaction. We can, however, calculate E_eq by combining the two Nernst equations. To do so we recognize that the poten- tials for the two half-reactions are the same; thus

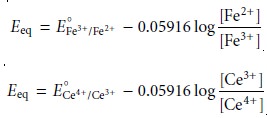
Adding together these two Nernst equations leaves us with

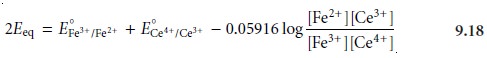
At the equivalence point, the titration reaction’s stoichiometry requires that

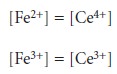
The ratio in the log term of equation 9.18, therefore, equals one and the log term is zero. Equation 9.18 simplifies to

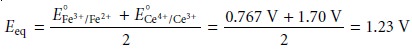
After the equivalence point, the concentrations of Ce3+ and excess Ce4+ are easy to calculate. The potential, therefore, is best calculated using the Nernst equation for the titrant’s half-reaction.

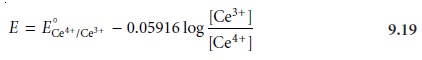
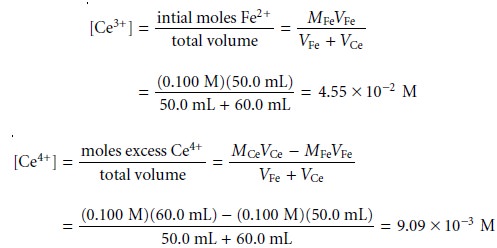
Substituting these concentrations into equation 9.19 gives the potential as

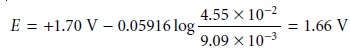
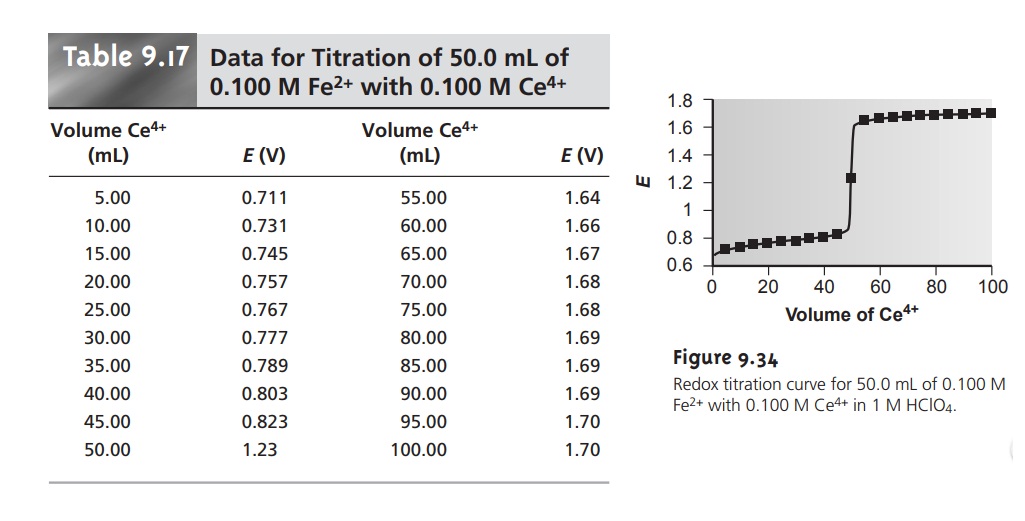
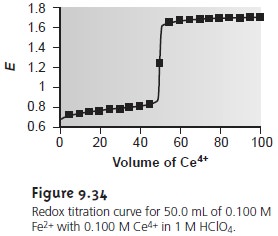
Additional results for this titration curve are shown in Table 9.17 and Figure 9.34

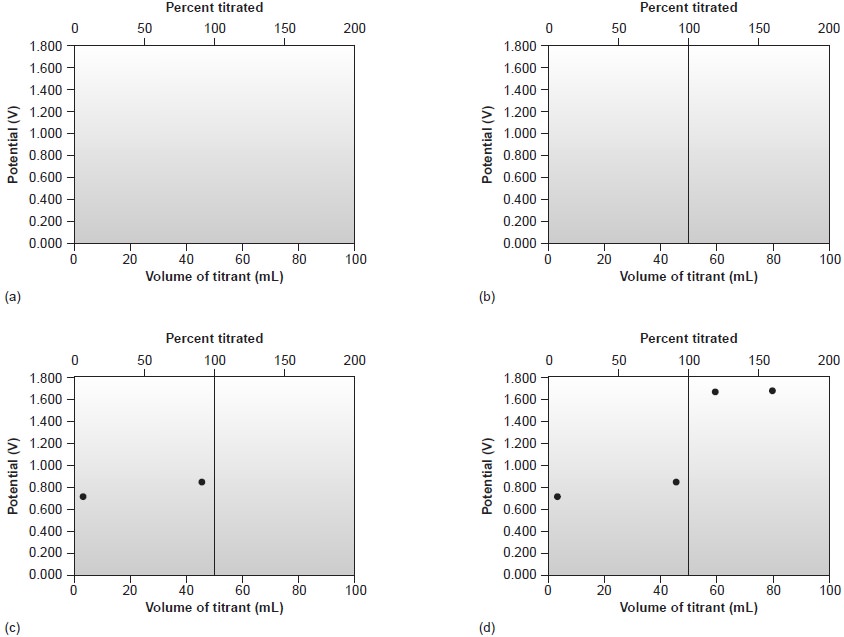
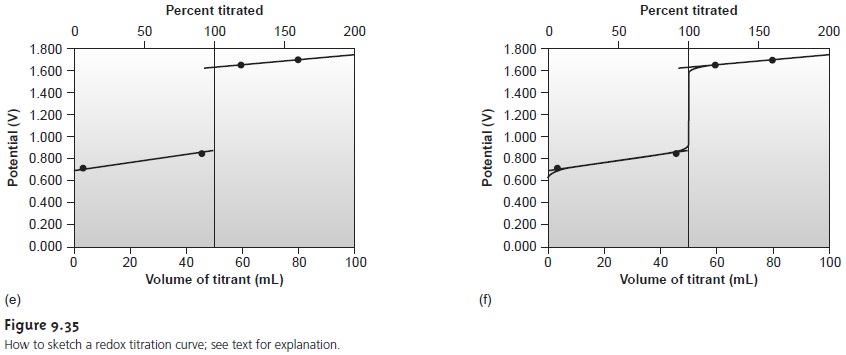
Sketching a Redox Titration Curve 

As we have done for acid–base and complexo- metric titrations, we now show how to quickly sketch a redox titration curve using a minimum number of calculations.