Chemistry and Properties of EDTA

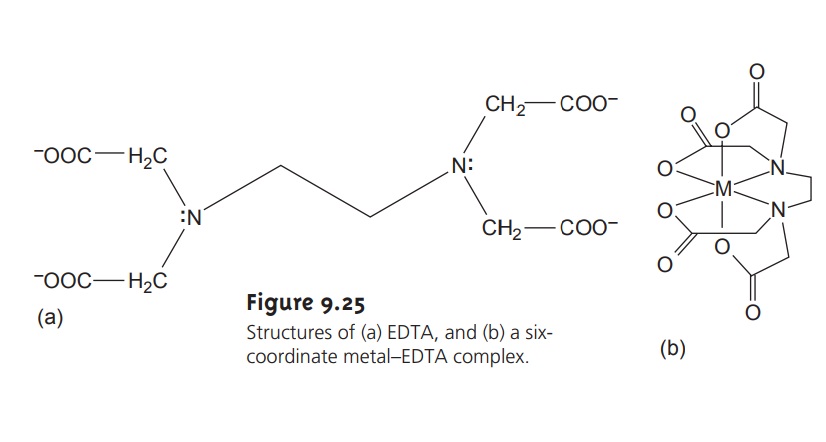
Chemistry and Properties of EDTA

Ethylenediaminetetraacetic acid, or EDTA, is an aminocar- boxylic acid. The structure of EDTA is shown in Figure 9.25a. EDTA, which is a Lewis acid, has six binding sites (the four car- boxylate groups and the two amino groups), providing six pairsof electrons. The resulting metal–ligand complex, in which EDTA forms a cage-like structure around the metal ion (Figure 9.25b), is very stable. The actual number of coordination sites depends on the size of the metal ion; however, all metal–EDTA complexes have a 1:1 stoichiometry.

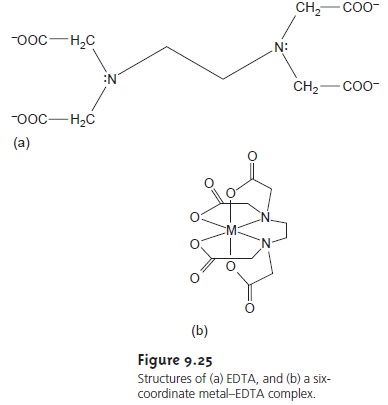
Metal–EDTA Formation Constants 

To illustrate the formation of a metal–EDTA complex consider the reaction between Cd2+ and EDTA

Cd2+(aq)+ Y4–(aq) t< == è CdY2–(aq)

where Y4– is a shorthand notation for the chemical form of EDTA shown in Figure 9.25. The formation constant for this reaction

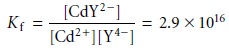                  9.11

is quite large, suggesting that the reaction’s equilibrium position lies far to the right. Formation constants for other metal–EDTA complexes are found in Appendix 3C.

EDTA Is a Weak Acid 

Besides its properties as a ligand, EDTA is also a weak acid. The fully protonated form of EDTA, H₆Y2+, is a hexaprotic weak acid with succes- sive pK_a values of

pK_a1 = 0.0 pK_a2 = 1.5 pK_a3 = 2.0 pK_a4 = 2.68 pK_a5 = 6.11 pK_a6 = 10.17

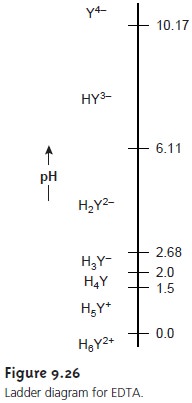
The first four values are for the carboxyl protons, and the remaining two values are for the ammonium protons. A ladder diagram for EDTA is shown in Figure 9.26. The species Y4– becomes the predominate form of EDTA at pH levels greater than 10.17. It is only for pH levels greater than 12 that Y4– becomes the only significant form of EDTA.

Conditional Metal–Ligand Formation Constants 

Recognizing EDTA’s acid–base properties is important. The formation constant for CdY2– in equation 9.11 as- sumes that EDTA is present as Y4–. If we restrict the pH to levels greater than 12, then equation 9.11 provides an adequate description of the formation of CdY2–. For pH levels less than 12, however, K_f overestimates the stability of the CdY2– complex.

At any pH a mass balance requires that the total concentration of unbound EDTA equal the combined concentrations of each of its forms.

C_EDTA = [H₆Y2+]+ [H₅Y+]+ [H₄Y]+ [H₃Y–]+ [H₂Y2–] + [HY3–]+ [Y4–]

To correct the formation constant for EDTA’s acid–base properties, we must ac count for the fraction, α_Y4–, of EDTA present as Y⁴–.

                           9.12

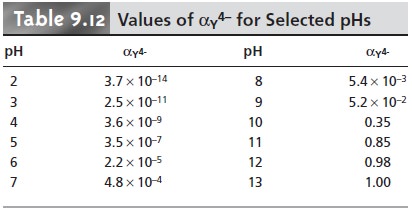
Values of α_Y4– are shown in Table 9.12. Solving equation 9.12 for [Y4–] and substi- tuting into the equation for the formation constant gives

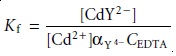
If we fix the pH using a buffer, then α_Y4– is a constant. Combining α_Y4– with K_f

gives

                     9.13

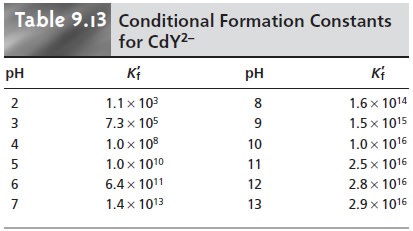
where K_f´ is a conditional formation constant whose value depends on the pH. As shown in Table 9.13 for CdY2–, the conditional formation constant becomes smaller, and the complex becomes less stable at lower pH levels.

EDTA Must Compete with Other Ligands 

To maintain a constant pH, we must add a buffering agent. If one of the buffer’s components forms a metal–ligand complex with Cd2+, then EDTA must compete with the ligand for Cd2+. For example, an NH₄+/NH₃ buffer includes the ligand NH₃, which forms several stable Cd2+–NH₃ complexes. EDTA forms a stronger complex with Cd2+ and will displace NH₃. The presence of NH₃, however, decreases the stability of the Cd2+–EDTA complex.

We can account for the effect of an auxiliary complexing agent, such as NH₃, in the same way we accounted for the effect of pH. Before adding EDTA, a mass balance on Cd2+ requires that the total concentration of Cd2+, C_Cd, be

C_Cd = [Cd2+] + [Cd(NH₃)2+] + [Cd(NH₃) 2+] + [Cd(NH₃) 2+] + [Cd(NH₃) 2+]

The fraction, α_Cd2+, present as uncomplexed Cd2+ is

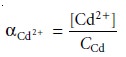               9.14

Solving equation 9.14 for [Cd2+] and substituting into equation 9.13 gives

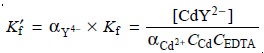
If the concentration of NH₃ is held constant, as it usually is when using a buffer, then we can rewrite this equation as

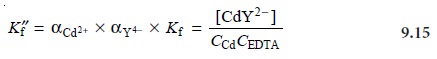
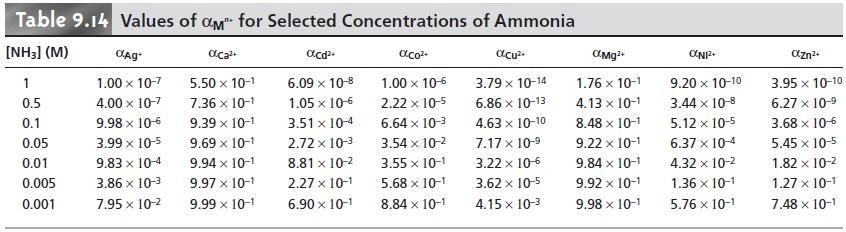
where K_f˝ is a new conditional formation constant accounting for both pH and the presence of an auxiliary complexing agent. Values of α_Mn+ for several metal ions are provided in Table 9.14.