Optimizing Chromatographic Separations Using the Capacity Factor to Optimize Resolution

Using the Capacity Factor to Optimize Resolution

One of the simplest ways to improve resolution is to adjust the capacity factor for solute B. If all other terms in equation 12.21 remain constant, increasing k_B’ improves resolution. As shown in Figure 12.11, however, the effect is greatest when the original capacity factor is small. 

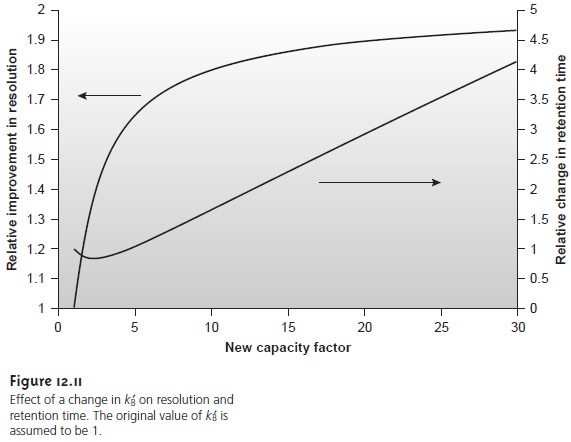
Furthermore, large increases in k_B’ do not lead to proportionally larger increases in resolution. For example, when the original value of k_B’ is 1, increasing its value to 10 gives an 82% improvement in resolution; a fur- ther increase to 15 provides a net improvement in resolution of only 87.5%.

Any improvement in resolution obtained by increasing k_B’ generally comes at the expense of a longer analysis time. This is also indicated in Figure 12.11, which shows the relative change in retention time as a function of the new capacity factor. Note that a minimum in the retention time curve occurs when k_B’ is equal to 2, and that retention time increases in either direction. Increasing k_B’ from 2 to 10, for ex- ample, approximately doubles solute B’s retention time.

The relationship between capacity factor and analysis time can be advantageous when a separation produces an acceptable resolution with a large k_B’. In this case it may be possible to decrease k_B’ with little loss in resolution while significantly short- ening the analysis time.

A solute’s capacity factor is directly proportional to its distribution ratio (equa- tion 12.6), which, in turn, is proportional to the solute’s equilibrium distribution constant. To increase k_B’ without significantly changing α, which also is a function of k_B’, it is necessary to alter chromatographic conditions in a way that leads to a general, nonselective increase in the capacity factor for both solutes. In gas chro- matography, this is usually accomplished by decreasing the column’s temperature. At a lower temperature a solute’s vapor pressure decreases, ensuring that it spends more time in the stationary phase increasing its capacity factor. In liquid chro- matography, changing the mobile phase’s solvent strength is the easiest way to change a solute’s capacity factor. When the mobile phase has a low solvent strength, solutes spend proportionally more time in the stationary phase, thereby increasing their capacity factors. Additionally, equation 12.6 shows that the capacity factor is proportional to the volume of stationary phase. Increasing the volume of stationary phase, therefore, also leads to an increase in k_B’.

Adjusting the capacity factor to improve resolution between one pair of solutes may lead to an unacceptably long retention time for other solutes. 

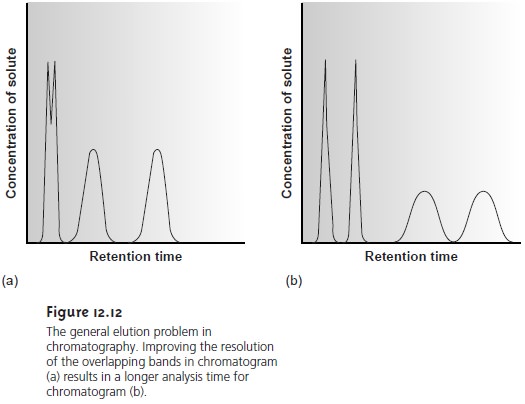
For ex- ample, improving resolution for solutes with short retention times by increasing on the other hand, decreasing k_B’ as a means of shortening the overall analysis time may lead to a loss of resolution for solutes eluting with shorter retention times. This difficulty is encountered so frequently that it is known as the general elution problem (Figure 12.12). One solution to the general elution problem is to make incremental adjustments to the capacity factor over time. Thus, initial chromato- graphic conditions are adjusted to enhance the resolution for solutes with short retention times. As the separation progresses, chromatographic conditions are changed in a manner that increases the elution rate (decreases the retention time) for later eluting solutes. In gas chromatography this is accomplished by tempera- ture programming. The column’s initial temperature is selected such that the first solutes to elute are fully resolved. The temperature is then increased, either continuously or in steps, to bring off later eluting components with both an ac- ceptable resolution and a reasonable analysis time. In liquid chromatography the same effect can be obtained by increasing the solvent’s eluting strength. This is known as a gradient elution.