Capacity Factor - Theory of Column Chromatography

Capacity Factor

The distribution of a solute, S, between the mobile phase and stationary phase can be represented by an equilibrium reaction

S_m < = = = = > S_s

and its associated partition coefficient, K_D, and distribution ratio, D,

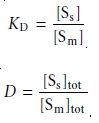                  12.2

where the subscripts m and s refer to the mobile phase and stationary phase, respec- tively. As long as the solute is not involved in any additional equilibria in either the mobile phase or stationary phase, the equilibrium partition coefficient and the dis- tribution ratio will be the same.

Conservation of mass requires that the total moles of solute remain constant throughout the separation, thus

(moles S)_tot = (moles S)_m + (moles S)_s    …………..12.3

Solving equation 12.3 for the moles of solute in the stationary phase and substitut- ing into equation 12.2 gives

where V_m and V_s are the volumes of the mobile and stationary phases. Rearranging and solving for the fraction of solute in the mobile phase, f_m, gives

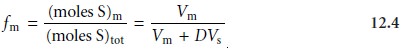
Note that this equation is identical to that describing the extraction of a solute in a liquid–liquid extraction. Since the volumes of the sta- tionary and mobile phase may not be known, equation 12.4 is simplified by dividing both the numerator and denominator by V_m; thus

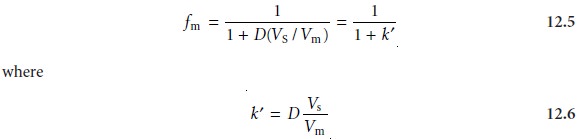
is the solute’s capacity factor.

A solute’s capacity factor can be determined from a chromatogram by measur- ing the column’s void time, t_m, and the solute’s retention time, t_r (see Figure 12.7). The mobile phase’s average linear velocity, u, is equal to the length of the column, L, divided by the time required to elute a nonretained solute.

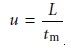                        12.7

By the same reasoning, the solute’s average linear velocity, v, is

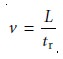                      12.8

The solute can only move through the column when it is in the mobile phase. Its average linear velocity, therefore, is simply the product of the mobile phase’s aver- age linear velocity and the fraction of solute present in the mobile phase.

v = uf_m ………………12.9

Substituting equations 12.5, 12.7, and 12.8 into equation 12.9 gives

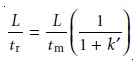
Finally, solving this equation for k’ gives

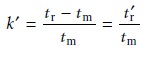                          12.10

where t_r’ is known as the adjusted retention time.