Optimizing Chromatographic Separations Using Column Efficiency to Optimize Resolution

Using Column Efficiency to Optimize Resolution

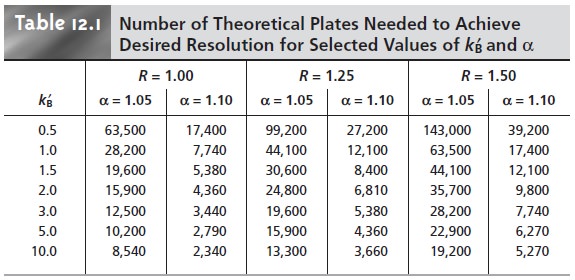
If the capacity factor and α are known, then equation 12.21 can be used to calculate the number of theoretical plates needed to achieve a desired resolution (Table 12.1). For example, given α = 1.05 and k_B’ = 2.0, a resolution of 1.25 requires approxi- mately 24,800 theoretical plates. If the column only provides 12,400 plates, half of what is needed, then the separation is not possible. How can the number of theoret- ical plates be doubled? The easiest way is to double the length of the column; how- ever, this also requires a doubling of the analysis time. A more desirable approach is to cut the height of a theoretical plate in half, providing the desired resolution with- out changing the analysis time. Even better, if H can be decreased by more than 50%, it also may be possible to achieve the desired resolution with an even shorter analysis time by decreasing k_B’ or α.

To determine how the height of a theoretical plate can be decreased, it is neces- sary to understand the experimental factors contributing to the broadening of a solute’s chromatographic band. Several theoretical treatments of band broadening have been proposed. We will consider one approach in which the height of a theo- retical plate is determined by four contributions: multiple paths, longitudinal diffu- sion, mass transfer in the stationary phase, and mass transfer in the mobile phase.

Multiple Paths

Solute molecules passing through a chromatographic column travel separate paths that may differ in length. Because of these differences in path length, solute molecules injected simultaneously elute at different times. The princi- pal factor contributing to this variation in path length is a nonhomogeneous pack- ing of the stationary phase in the column. Differences in particle size and packing consistency cause solute molecules to travel paths of different length. Some solute molecules follow relatively straight paths through the column, but others follow a longer, more tortuous path (Figure 12.14a). The contribution of multiple paths to the height of a theoretical plate, H_p, is

H_p = 2λd_p………………12.23

where d_p is the average diameter of the particulate packing material, and λ is a con-stant accounting for the consistency of the packing. A smaller range of particle sizes and a more consistent packing produce a smaller value for λ. Note that for an open tubular column, which does not contain packing material, H_p is 0.

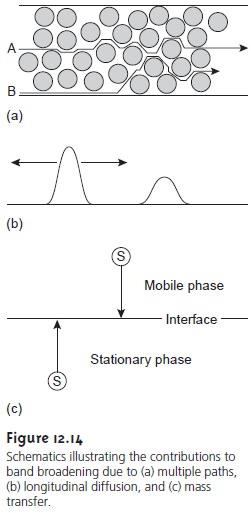
Longitudinal Diffusion 

The second contribution to band broadening is the result of the solute’s longitudinal diffusion in the mobile phase. Even if the mobile phase velocity is 0, solute molecules are constantly in motion, diffusing through the mo- bile phase. Since the concentration of solute is greatest at the center of a chromato- graphic band, more solute diffuses toward the band’s forward and rear edges than diffuses toward the band’s center. The net result is an increase in the band’s width (Figure 12.14b). The contribution of longitudinal diffusion to the height of a theo- retical plate, H_d, is

where D_m is the solute’s diffusion coefficient in the mobile phase, u is the mobile phase velocity, and γ is a constant related to the column packing. The effect of H_d on the height of a theoretical plate is minimized by a high mobile-phase velocity. Because a solute’s diffusion coefficient is larger in a gaseous mobile phase than in a liquid mobile phase, longitudinal diffusion is a more serious problem in gas chromatography.

Mass Transfer 

The final two contributions to band broadening result from the fi- nite time required for a solute molecule to diffuse through the stationary phase and mobile phase. A chromatographic separation occurs because solutes move between the stationary and mobile phases. For a solute to move from one phase to the other, it must first diffuse to the interface between the two phases (Figure 12.14c)—a process called mass transfer. A contribution to band broadening occurs whenever the solute’s movement to the interface is not fast enough to maintain a true equilib- rium distribution of solute between the two phases. Thus, solute molecules in the mobile phase move farther down the column than expected before passing into the stationary phase. Solute molecules in the stationary phase, on the other hand, take longer than expected to cross into the mobile phase. The contributions of mass transfer in the stationary phase, H_s, and mass transfer in the mobile phase, H_m, are given by

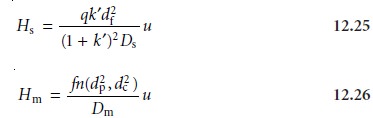
where d_f is the thickness of the stationary phase, d_c is the column’s diameter, D_s is the solute’s diffusion coefficient in the stationary phase, q is a constant related to the column packing material, and the remaining terms are as previously defined. As in- dicated in equation 12.26, the exact form of H_m is unknown, although it is a func- tion of particle size and column diameter. The contribution of mass transfer to the height of a theoretical plate is smallest for slow mobile-phase velocities, smaller di- ameter packing materials, and thinner films of stationary phase.

Putting It All Together 

The net height of a theoretical plate is a summation of the contributions from each of the terms in equations 12.23–12.26; thus,

H = H_p+ H_d + H_s + H_m………………12.27

An alternative form of this equation is the van Deemter equation

which emphasizes the importance of the mobile phase’s flow rate. In the van Deemter equation, A accounts for multiple paths (H_p), B/u for longitudinal diffusion (H_d), and Cu for the solute’s mass transfer in the stationary and mobile phases (H_s and H_m).

There is some disagreement on the correct equation for describing the relation- ship between plate height and mobile-phase velocity. In addition to the van Deemter equation (equation 12.28), another equation is that proposed by Hawkes

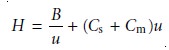
where C_s and C_m are the mass transfer terms for the stationary and mobile phases respectively. A third equation was devised by Knox.

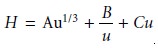
All three equations, and others, have been used to characterize chromatographic systems, with no single equation providing the best explanation in every case.

To increase the number of theoretical plates without increasing the length of the column, it is necessary to decrease one or more of the terms in equation 12.27 or equation 12.28. The easiest way to accomplish this is by adjusting the velocity of the mobile phase. At a low mobile-phase velocity, column efficiency is limited by longitudinal diffusion, whereas at higher velocities efficiency is limited by the two mass transfer terms. 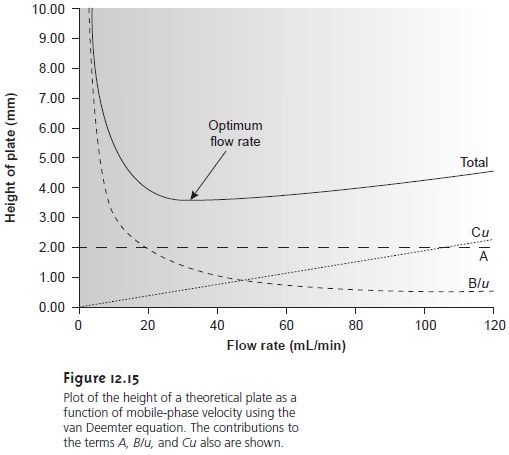As shown in Figure 12.15 (which is interpreted in terms of equation 12.28), the optimum mobile-phase velocity corresponds to a minimum in a plot of H as a function of u.

The remaining parameters affecting the height of a theoretical plate are deter- mined by the construction of the column and suggest how the column’s design may be used to improve efficiency. For example, both H_p and H_m are a function of the size of the particles used for the packing material. Decreasing particle size, therefore, is one approach to improving efficiency. A decrease in particle size is limited, however, by the need for a greater pressure to push the mobile phase through the column.

One of the most important advances in column construction has been the de- velopment of open tubular, or capillary columns that contain no packing material (d_p = 0). Instead, the interior wall of a capillary column is coated with a thin film of the stationary phase. The absence of packing material means that the mobile phase can move through the column with substantially less pressure. 

As a result, capillary columns can be manufactured with much greater lengths than is possible with a packed column. Furthermore, plate height is reduced because the H_p term in equation 12.27 disappears and the H_m term becomes smaller. The combination of a smaller height for a theoretical plate and a longer column leads to an approximate 100-fold increase in the number of theoretical plates. Capillary columns are not without disadvantages. Because capillary columns are much narrower than packed columns, they require a significantly smaller amount of sample. Difficulties with re- producibly injecting small samples complicates the use of capillary chromatography for quantitative work.

Another approach to improving resolution is to use thin films of stationary phase. Capillary columns used in gas chromatography and the bonded phases com- monly used in HPLC provide a significant decrease in plate height due to the reduc- tion of the H_s term in equation 12.27.