Numerical Problems

Short Answer Questions

Example

A conductivity cell has two platinum electrodes separated by a distance 1.5 cm and the cross sectional area of each electrode is 4.5 sq cm. Using this cell, the resistance of 0.5 N electrolytic solution was measured as 15 Ω . Find the specific conductance of the solution.

Solution

l = 1 5. cm = 1.5×10-2 m

A = 4.5 cm2 = 4.5×(10-4)m2

R = 15Ω

κ = 1/R (l/A)

κ = [ 1/15Ω ] × [1.5×10-2 m  / 4.5×(10-4)m2 ]

= 2.22 Sm-1

Example

Calculate the molar conductance of 0.025M aqueous solution of calcium chloride at 25º C. The specific conductance of calcium chloride is 12.04 Ã— 10-2 Sm-1.

Molar conductance = Î› m =

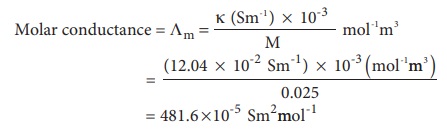
 = 481.6 Ã—10-5 Sm2mol-1

Example

The resistance of a conductivity cell is measured as 190 Ω using 0.1M KCl solution (specific conductance of 0.1M KCl is 1.3 Sm-1 ) . When the same cell is filled with 0.003M sodium chloride solution, the measured resistance is 6.3KΩ. Both these measurements are made at a particular temperature. Calculate the specific and molar conductance of NaCl solution.

Given that

κ = 1.3 Sm-1 (for 0.1M KCl solution)

R = 190 Ω

Λm = 13.04 Ã— 10-3 Sm2 mol-1

Example

A solution of silver nitrate is electrolysed for 20 minutes with a current of 2 amperes. Calculate the mass of silver deposited at the cathode.

Electrochemical reaction at cathode is Ag+ +e- â†’ Ag (reduction)

Book Back Questions and Answers

8. The conductivity of a 0.01M solution of a 1 :1 weak electrolyte at 298K is 1.5 ×10^-4 S cm^−1.

i) molar conductivity of the solution

ii) degree of dissociation and the dissociation constant of the weak electrolyte

Given that

λº_cation = 248.2 S cm² mol^−1

λº_cation = 51.8 S cm² mol^−1

Answer:

Given

C = 0.01M 

λº_cation = 248.2 S cm² mol^−1

K= 1.5 × 10^−4 S cm^−1

λº_anion = 51.8 S cm² mol^−1.

1. Molar conductivity

K = 1.5 ×10^−4 S cm^−1

Λºm =  K(sm^−1 ) ×10^−3 / C (in M) mol^-1 m³

= (1.5 ×10² ×10^−3 ) / 0.01 S mol ^−1 m²      1 cm^−1 = 10²m^−1

= 1.5 ×10^−3 S m² mol^−1 = 1.5 ×10²

2. Degree of dissociation α = Λº/Λº_∞

Λ^o_∞ =λ^o_cation +λ_anion^o

= (248.2 + 51.8) S cm² mol^−1

= 300 S cm² mol^−1

= 300 ×10^−14 s m² mol^−1

α = 1.5 ×10^−3 S m² mol^−1  / 300×10^−4 S m² mol^−1

α = 0.05

K_a = α²c / 1-α

= [ (0.05)² (0.01) ] / 1-0.05

= 25 ×10^−4 ×10^−2 /  95 ×10^−2

= 0.26 ×10^−4

= 2.6 ×10^−5.

13. A current of 1.608A is passed through 250 mL of 0.5M solution of copper sulphate for 50 minutes. Calculate the strength of Cu²⁺ after electrolysis assuming volume to be constant and the current efficiency is 100%.

Answer:

Given

I = 1.608A; t = 50 min = 50 × 60

= 3000S

 Î· = 100%

V=250 mL

C=0.5M

 Calculate the number of faradays of electricity passed through the CuSO₄ solution

⇒ Q=It

 Q = 1.608 ×3000

Q = 4824C

∴ number of Faradays of electicity = 4824 C  / 96500C = 0.05F

Electrolysis of CuSO₄

Cu²⁺ (aq)+2e^− → Cu(s).

The above equation shows that 2F electricity will deposit 1 mole of Cu²⁺ to Cu.

∴0.05F electricity will

deposit  1 mol /2F × 0 .05F = 0.025 mol

Initial number of molar of Cu²⁺ in 250 ml of solution = (0.5 / 1000 mL)  × 250mL

= 0.125 mol

∴ number of moles of Cu²⁺ after electrolysis = 0.125 - 0.025

= 0.1 mol

∴ Concentration of Cu²⁺ = [ 0.1 mol/ 250 mL ] ×1000 mL

=0.4M

14. Can Fe³⁺ oxidises bromide to bromine under standard conditions?

Given: E_{Fe 3+|Fe2+} = 0.771

E_Br2|Br− = 1.09V.

Answer:

Required half cell reaction

2 Br^- → Br₂ + 2e^−

( E^o_ox )= −1.09V

2 Fe³⁺ + 2e^− → 2Fe²⁺

( E^o_red )= +0.771V

2Fe³⁺ + 2Br^− → 2Fe²⁺ +Br₂

( E^o_cell )= ?

E^o_cell = ( E^o_ox )+ ( E^o_red )

 = −1.09 + 0.771

−0.319V

E_cell is – ve; ∆G is +ve and the cell reaction is non spontaneous. Hence Fe³⁺ cannot oxidises Br^- to Br₂

15. Is it possible to store copper sulphate in an iron vessel for a long time?

Given : E_{Cu 2+|Cu} = 0.34 V and E_{Fe 2+|Fe} = −0.44V .

Answer:

 ( E_ox^o )_Fe|Fe2+ = 0.44V and ( E_red^o )_{Cu 2+|Cu} = 0.34V .

These +ve emf values shows that iron will oxidise and copper will get reduced i.e., the vessel will dissolve.

Hence it is not possible to store copper sulphate in an iron vessel.

16. Two metals M₁ and M₂ have reduction potential values of -xV and +yV respectively. Which will liberate H₂ and H₂SO₄.

Answer:

Metals having higher oxidation potential will liberate H₂ from H₂ SO₄ . Hence, the metal M₁ having + xV, oxidation potential will liberate H₂ from H₂SO₄ .

17. Reduction potential of two metals M and M₂ are Eº_M12+|M1 = − 2.3V and E Eº_M22+|M2 = 0.2V  Predict which one is better for coating the surface of iron. Given : E _{Fe2+ |Fe} = −0.44V

Answer:

oxidation potential of M₁ is more +ve than the oxidation potential of Fe which indicates that it will prevent iron from rusting

18. Calculate the standard emf of the cell: Cd | Cd ²⁺ || Cu ²⁺ | Cu and determine the cell reaction. The standard reduction potentials of Cu²⁺ | Cu and Cd²⁺ | Cd are 0.34V and -0.40 volts respectively. Predict the feasibility of the cell reaction.

Answer:

Cell reactions:

Oxidation at anode: Cd (s) → Cd²⁺ (aq) + 2e^−

( E^o_ox) _Cu|Cd2+ = 0.4V

Reduction at cathode: Cu²⁺ (aq) + 2e^- → Cu (s)

( E^o_red )_Cu2+|Cu = 0.34V

Cd ( s ) + 2e^- → Cd²⁺ (aq) + Cu(s)

E_cell = ( E^o_ox )+ ( E_red^o )_cathode

= 0.4 + 0.34

= 0.74V.

emf is +ve, so ∆G is (-)ve, the reaction is feasible.

19. In fuel cell H₂ and O₂ react to produce electricity. In the process, H₂ gas is oxidised at the anode and O₂ at cathode. If 44.8 litre of H₂ at 25^oC and 1atm pressure reacts in 10 minutes, what is average current produced? If the entire current is used for electro deposition of Cu from Cu²⁺ , how many grams of Cu deposited?

Answer:

Oxidation at anode:

2H₂ (g) + 4OH^- (aq) → 4H₂O (l) + 4e^−

1 mole of hydrogen gas produces 2 moles of electrons at 25º C and 1 atm pressure, 1 mole of hydrogen gas occupies = 22.4 litres

∴ no. of moles of hydrogen gas produced = [1 mole / (22.4 litres)] × 44.8 litres

 = 2 moles of hydrogen

∴ 2 of moles of hydrogen produces 4 moles of electron i.e., 4F charge.

We know that Q= It

I= Q/t

= 4F / 10 mins

= 4×96500 C / 10×60 s

I=643.33 A

Electro deposition of copper

Cu²⁺ (aq)+2e^- → Cu(s)

2F charge is required to deposit

1 mole of copper i.e., 63.5 g

If the entire current produced in the fuel cell ie., 4 F is utilised for electrolysis, then 2× 63.5 i.e., 127.0 g copper will be deposited at cathode.

20. The same amount of electricity was passed through two separate electrolytic cells containing solutions of nickel nitrate and chromium nitrate respectively. If 2.935g of Ni was deposited in the first cell. The amount of Cr deposited in the another cell? Give : molar mass of Nickel and chromium are 58.74 and 52gm^-1 respectively.

Answer:

Ni²⁺ (aq) + 2e^- → Ni (s)

Cr²⁺ (aq)+3e^− → Cr (s)

The above reaction indicates that 2F charge is required to deposit 58.7g of Nickel form nickel nitrate and 3F charge is required to deposit 52g of chromium.

Given that 2.935 gram of Nickel is deposited

∴The amount of charge passed through the cell = (2F/58.7 g) × 2.935g

= 0.1F

∴ if 0.1F charge is passed through chromium nitrate the amount of chromium deposited = 52g/3F × 0.1F

 = 1.733g

21. A copper electrode is dipped in 0.1M copper sulphate solution at 25^oC . Calculate the electrode potential of copper. [Given: E_{Cu 2+|Cu} = 0.34 V ].

Answer:

Given that

[ Cu²⁺] = 0.1M

Eº_{Cu2+ |Cu} = 0.34

Ecell = ?

Cell reaction is

Cu²⁺ (aq) + 2e^− → Cu (s)

E_cell = E^o – [0.0591/n] log {[Cu] [Cu²⁺]}

= 0.34 – [0.0591/2] log (1/0.1)

 = 0.34 −0.0296

 = 0.31V

22. For the cell Mg (s) | Mg²⁺ (aq) || Ag⁺ (aq) | Ag (s), calculate the equilibrium constant at  25^oC and maximum work that can be obtained during operation of cell. Given : Eº _{Mg 2+ | Mg} = −2.37V and Eº_{Ag + | Ag} = 0.80V.

Answer:

oxidation at anode

Mg → Mg²⁺ +2e^-    .............. (1)   ( Eº_xo) = 2.37V

Reduction at cathode

Ag⁺ + e^- → Ag ........... (2) ( Eº_red) = 0.80V

∴ Eº_cell = ( Eº_ox )_anode + ( Eº_red )_cathode

= 2.37+0.80

= 3.17V

Overall reaction

Equation (1) + 2 × equation ( 2 ) ⇒

Mg+ 2Ag²⁺ → Mg²⁺ + 2Ag

∆G = -nfE

=−2 × 96500 × 3.17

=−611810 J

∆G^o = −6.12 ×10⁵ J

W = 6.12 ×10⁵ J

∆G^o =−2.303 RT log^KC

∆G^o =−2.303 RT log^KC

⇒ log K_c = (6.12 ×10⁵) /  (2.303 × 8.314 × 298)

K_c = Antilog of (107.2)

23. 8.2 ×10¹² litres of water is available in a lake. A power reactor using the electrolysis of water in the lake produces electricity at the rate of 2 ×10⁶ Cs^−1 at an appropriate voltage. How many years would it like to completely electrolyse the water in the lake. Assume that there is no loss of water except due to electrolysis.

Answer:

Electrolysis of water

At anode:

2H₂O → 4H⁺ + O₂ + 4e^−      ......... (1)

At cathode:

2H₂ O+2e^− → H₂ + 2OH^-

Overall reaction 6H₂O → 4H⁺ + 4OH^- + 2H₂ + O₂

(or)

Equation (1) +(2) ×2 ⇒ 2H₂ O → 2H₂ + O₂

According to faradays Law of electrolysis, to electrolyse two mole of Water (36g = 36 mL of H₂O), 4F charge is required alternatively, when 36 mL of water is electrolysed, the charge generated = 4 × 96500 C.

When the whole water which is available on the lake is completely electrolysed the amount of charge generated is equal to (4 × 96500 C / 36 mL)  × 9 ×10¹² L

= ( 4 × 96500 × 9 ×10¹² ) / ( 36 ×10^−3 ) C

= 96500 ×10¹⁵ C

∴Given that in 1 second, 2 ×10⁶ C is generated therefore, the time required to generate

 96500 ×10¹⁵ C is = [ 1 S/  2 ×10⁶C]  × 96500 ×10¹⁵ C

= 48250 ×10⁹ S

1 year = 365 days

= 365 × 24 hours

= 365×24 × 60 min

1 year = 365×24 × 60 × 60 sec.

∴ Number of years = 48250 ×10⁹ / 365×24×60×60

 = 1.5299 ×10⁶ years