Variation of molar conductivity with concentration | Electro Chemistry - Kohlraush's law and its Applications | 12th Chemistry : UNIT 9 : Electro Chemistry
Chapter: 12th Chemistry : UNIT 9 : Electro Chemistry
Kohlraush's law and its Applications
Kohlraush's law
The limiting molar conductance ╬ø0m is the basis for kohlraush law. At infinite dilution, the limiting molar conductivity of an electrolyte is equal to the sum of the limiting molar conductivities of its constituent ions. i.e., the molar conductivity is due to the independent migration of cations in one direction and anions in the opposite direction.
For a uni ŌĆō univalent electrolyte such as NaCl, the Kohlraush's law is expressed as
(╬ø0m )NaCl = ( ╬╗0m )Na+ + ( ╬╗0m )Cl-
In general, according to Kohlraush's law, the molar conductivity at infinite dilution for a electrolyte represented by the formula Ax By , is given below.
(╬ø0m)AxBy = x ( ╬╗0m )Ay+ + y ( ╬╗0m )Bx- .....(9.13)
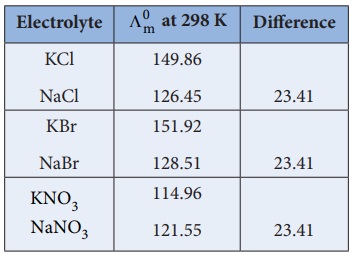
Kohlraush arrived the above mentioned relationship based on the experimental observations such as the one as shown in the table. These result show that at infinite dilution each constituent ion of the electrolyte makes a definite contribution towards the molar conductance of the electrolyte irrespective of nature of other ion with which it is associated
i.e.,
(╬ø┬║m )KCl ŌłÆ ( ╬ø┬║m)NaCl = 149.86 - 126.45
{( ╬╗┬║m )K+ + ( ╬╗┬║m )Cl- } ŌĆō {( ╬╗┬║m )Na+ + ( ╬╗┬║m)Cl- } = 23.41
( ╬╗┬║m ) K+ - ( ╬╗┬║m )Na+ = 23.41
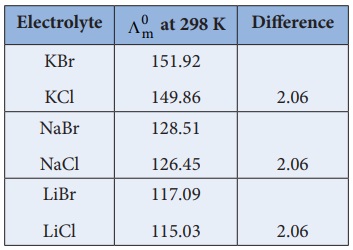
Similarly, we can conclude that ( ╬╗┬║m )Br- ŌłÆ ( ╬╗┬║m )Cl- = 2.06
Applications of Kohlrausch's Law
1. Calculation of molar conductance at infinite dilution of a weak electrolyte.
It is impossible to determine the molar conductance at infinite dilution for weak electrolytes experimentally. However, the same can be calculated using KohlraushŌĆÖs Law.
For example, the molar conductance of CH3COOH, can be calculated using the experimentally determined molar conductivities of strong electrolytes HCl, NaCl and CH3COONa .
╬ø┬║CH3COONa = ╬╗┬║Na+ + ╬╗┬║CHCOO- .....(1)
╬ø┬║HCl = ╬╗┬║H+ + ╬╗┬║Cl- .....(2)
╬ø┬║NaCl = ╬╗┬║Na+ + ╬╗┬║Cl- .....(3)
Equation (1) + Equation (2) ŌĆō Equation (3) gives,
╬ø┬║CH3COONa + ╬ø┬║HCl - ╬ø┬║NaCl = ╬╗oH+ + ╬╗oCH3COO-
= ╬ø┬║CH3COOH
2. Calculation of degree of dissociation of weak electrolytes
The degree of dissociation of weak electrolyte can be calculated from the molar conductivity at a given concentration and the molar conductivity at infinite dilution using the following expression

Calculation of dissociation constant using ╬øm values. According to Ostwald dilution Law,

Substitute ╬▒ value in the above expression ( 9.15)
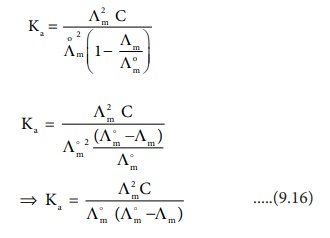
3. Calculation of solubility of sparingly soluble salts
Substances like AgCl, PbSO4 etc., are sparingly soluble in water. The solubility product of such substances can be determined using conductivity measurements.
Let us consider AgCl as an example
AgCl (s) Ōåö Ag+ + ClŌłÆ
Ksp = [Ag+ ][Cl- ]
Let the concentration of [Ag + ] be ŌĆśCŌĆÖ molLŌĆō1.
As per the stoichiometry, if [Ag+ ] = C, then [ClŌłÆ]also equal to ŌĆśCŌĆÖ mol LŌłÆ1 .
Ksp =C.C
Ksp = C2
We know that the concentration (in mol dm-3) is related to the molar and specific conductance by the following expressions
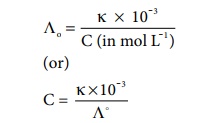
Substitute the concentration value in the relation Ksp = C2
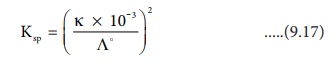
Related Topics