Electro Chemistry | Chemistry - Conductivity of electrolytic solution | 12th Chemistry : UNIT 9 : Electro Chemistry
Chapter: 12th Chemistry : UNIT 9 : Electro Chemistry
Conductivity of electrolytic solution
Conductivity of electrolytic solution
We have already learnt that when an electrolyte such as sodium chloride,
potassium chloride etc... is dissolved in a solvent like water, the electrolyte
is completely dissociated to give its constituent ions (namely cations and
anions). When an electric field is applied to such an electrolytic solution,
the ions present in the solution carry charge from one electrode to another
electrode and thereby they conduct electricity. The conductivity of the
electrolytic solution is measured using a conductivity cell. (Fig 9.1)
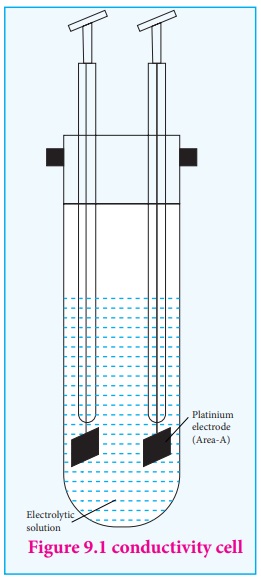
A conductivity cell consists of two electrodes immersed in an electrolytic solution. It obeys Ohm's law like metallic conductor. i.e., at a constant temperature, the current flowing through the cell (I) is directly proportional to the voltage across the cell (V).
i.e., I ╬▒ V
(or)
I = V/ R

ŌćÆ V=IR .....(9.1)
Where ŌĆśRŌĆÖ is the resistance of the solution in ohm (Ōä”) Here the
resistance is the opposition that a cell offers to the flow of electric current
through it.
Resistivity (Žü)
Let us consider a conductivity cell in which the electrolytic solution
is confined between the two electrodes having cross sectional area (A) and are
separated by a distance ŌĆślŌĆēŌĆÖ . Like
the metallic conductor, the resistance of such an electrolytic solution is also
directly proportional to the length (lŌĆē)
and inversely proportional to the cross sectional area (A).
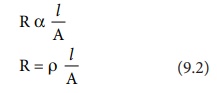
Where Žü (rho) is
called the specific resistance or resistivity, which depends on the nature of
the electrolyte.
If l/A = 1 m-1,
then, Žü = R .
Hence the resistivity is defind as the resistance of an electrolyte confined
between two electrodes having unit cross sectional area and are separated by a
unit distance. The ratio (l/A) is called the cell constant, Unit
of resistivity is ohm metre (Ōä”m).
Conductivity
It is more convenient to use conductance rather than resistance. The
reciprocal of the resistance (1/R) gives the conductance of an electrolytic
solution. The SI unit of conductance is Siemen (S) .
C = 1/R ..... (9.3)
Substitute (R) from (9.2) in (9.3)
ŌćÆ i.e., C = 1/Žü . A/l . .....(9.4)

The reciprocal of the specific resistance ( 1/Žü) is called the
specific conductance (or) conductivity. It is represented by the symbol ╬║appa (╬║) .
Substitute 1/Žü = ╬║ in equation (9.4) and rearranging
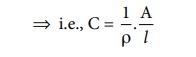
╬║ = C
. (l/A) ŌĆ”ŌĆ”.(9.5)
If A = 1m2 and l = 1m ; then ╬║ = C.
The specific conductance is defined as the conductance of a cube of an
electrolytic solution of unit dimensions (Fig 9.2). The SI unit of specific
conductance is Sm-1 .

Example
A conductivity cell has two platinum electrodes separated by a distance
1.5 cm and the cross sectional area of each electrode is 4.5 sq cm. Using this
cell, the resistance of 0.5 N electrolytic solution was measured as 15 Ōä” . Find
the specific conductance of the solution.
Solution
l = 1 5.
cm = 1.5├Ś10-2 m
A = 4.5 cm2 = 4.5├Ś(10-4)m2
R = 15Ōä”
╬║ = 1/R (l/A)
╬║ = [ 1/15Ōä” ] ├Ś [1.5├Ś10-2 m / 4.5├Ś(10-4)m2
]
= 2.22 Sm-1
Molar conductivity (╬øm )
Solutions of different concentrations have different number of
electrolytic ions in a given volume of solution and hence they have different
specific conductance. Therefore a new quantity called molar conductance (╬øm ) was
introduced.
Let us imagine a conductivity cell in which the electrodes are separated
by 1m and having V m3 of electrolytic solution which contains 1 mole
of electrolyte. The conductance of such a system is called the molar
conductance (╬øm ).
We have just learnt that the conductance of 1 m3 electrolytic
solution is called the specific conductance (╬║) . Therefore, the conductance of the above
mentioned V m3 solution (╬øm ) is given by the following expression.
(╬ø m
) = ╬║ ├Ś V .....(9.6)
We know that, molarity (M) = Number of moles of solute (n) / Volume of
the solution (V in dm3 )
Therefore, Volume of the solution containing one mole of solute = 1 / M (
mol-1 L)
Ōł┤ Volume per m3 (V) = 10-3/M ( mol -1
m3 )
Substitute (9.7) in (9.6)
(9 .6) ŌćÆ ╬øm = { ╬║ (Sm-1)
├Ś 10-3}/M mol-1 m-3 .....(9.8)
The above relation defines the molar conductance in terms of the
specific conductance and the concentration of the electrolyte.
Example
Calculate the molar conductance of 0.025M aqueous solution of calcium
chloride at 25┬║ C. The
specific conductance of calcium chloride is 12.04 ├Ś 10-2
Sm-1.
Molar conductance = ╬ø m
=
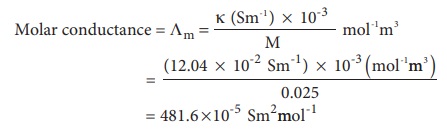
= 481.6 ├Ś10-5
Sm2mol-1
Evaluate yourself : 1
Calculate the molar conductance of 0.01M aqueous KCl
solution at 25┬║ C . The specific conductance of KCl at 25┬║C is 14.114 ├Ś10- 2 Sm-1 .
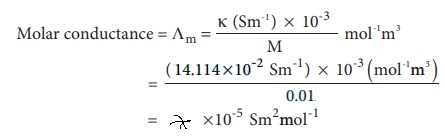
Equivalent conductance (╬ø)
Equivalent conductance is defined as the conductance of 'V' m3 of electrolytic solution containing one gram equivalent of electrolyte in a conductivity cell in which the electrodes are one metre apart.
The relation between the equivalent conductance and the specific
conductance is given below.
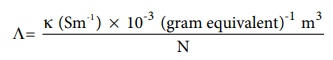
╬ø = { ╬║ (Sm-1) ├Ś 10-3 (gram
equivalent)-1 m3
} / N .....(9..9)
Where ╬║ the
specific conductance and N is the concentration of the electrolytic solution
expressed in normality.
Evaluate yourself : 2
The resistance of 0.15N solution of an electrolyte is 50 Ōä”. The specific
conductance of the solution is 2.4 Sm-1. The resistance of 0.5 N
solution of the same electrolyte measured using the same conductivity cell is
480 Ōä”. Find the equivalent conductivity of 0.5 N solution of the electrolyte.
Given that
R1=50Ōä”
R2= 480Ōä”
╬║1 = 2.4 Sm-1
╬║2 = ?
N1 = 0.15 N
N2 = 0.5 N

Factors affecting electrolytic conductance
If the interionic attraction between the oppositely charged ions of
solutes increases, the conductance will decrease.
ŌĆó Solvent of higher dielectric constant show high conductance in
solution.
ŌĆó Conductance is inversely proportional to the Viscosity of the medium.
i.e., conductivity increases with the decrease in viscosity.
ŌĆó If the temperature of the electrolytic solution increases, conductance
also increases. Increase in temperature increases the kinetic energy of the
ions and decreases the attractive force between the oppositely charged ions and
hence conductivity increases.
ŌĆó Molar conductance of a solution increases with increase in dilution.
This is because, for a strong electrolyte, interionic forces of attraction
decrease with dilution. For a weak electrolyte, degree of dissociation
increases with dilution.
Measurement of conductivity of ionic solutions
We have already learnt to measure the specific resistance of a metallic
wire using a metre bridge in your physics practical experiment. We know that it
works on the principle of wheatstone bridge. Similarly, the conductivity of an
electrolytic solution is determined by using a wheatstone bridge arrangement in
which one resistance is replaced by a conductivity cell filled with the
electrolytic solution of unknown conductivity.
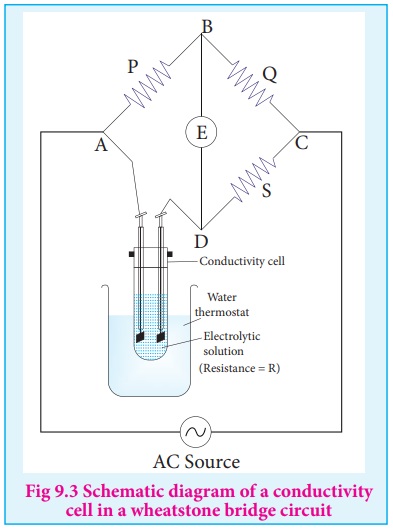
In the measurement of specific resistance of a metallic wire, a DC power
supply is used. Here, if we apply DC current through the conductivity cell, it will
lead to the electrolysis of the solution taken in the cell. So, AC current is
used for this measurement to prevent electrolysis.
A wheatstone bridge is constituted using known resistances P, Q, a variable
resistance S and conductivity cell (Let the resistance of the electrolytic solution
taken in it be R) as shown in the figure 9.3. An AC source (550 Hz to 5 KHz) is
connected between the junctions A and C. Connect a suitable detector E (Such as
the telephone ear piece detector) between the junctions ŌĆśBŌĆÖ and ŌĆśDŌĆÖ.
The variable resistance ŌĆśSŌĆÖ is adjusted until the bridge is balanced and
in this conditions there is no current flow through the detector.
Under balanced condition,
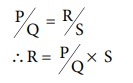
P/Q = R/S
R = P/Q ├Ś S ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”(9.10)
The resistance of the electrolytic solution (R) is calculated from the
known resistance values P, Q and the measured ŌĆśSŌĆÖ value under balanced
condition using the above expression (9.10).
Conductivity calculation
Specific conductance (or) conductivity of an electrolyte can be
calculated from the resistance value using the following expression.

The value of the cell constant l/A
is usually provided by the cell manufacturer. Alternatively the cell constant
may be determined using KCl solution whose concentration and specific
conductance are known.
Example
The resistance of a conductivity cell is measured as 190 Ōä” using 0.1M
KCl solution (specific conductance of 0.1M KCl is 1.3 Sm-1 ) . When
the same cell is filled with 0.003M sodium chloride solution, the measured
resistance is 6.3KŌä”. Both these measurements are made at a particular
temperature. Calculate the specific and molar conductance of NaCl solution.
Given that
╬║ = 1.3 Sm-1
(for 0.1M KCl solution)
R = 190 Ōä”

╬øm = 13.04 ├Ś 10-3
Sm2 mol-1
Related Topics