Explanation, Formulas, Solved Example Problems - KirchhoffŌĆÖs Second rule (Voltage rule or Loop rule) | 12th Physics : Current Electricity
Chapter: 12th Physics : Current Electricity
KirchhoffŌĆÖs Second rule (Voltage rule or Loop rule)
KirchhoffŌĆÖs Second rule (Voltage
rule or Loop rule)
It states that in a
closed circuit the algebraic sum of the products of the current and resistance
of each part of the circuit is equal to the total emf included in the circuit.
This rule follows from the law of conservation of energy for an isolated system
(The energy supplied by the emf sources is equal to the sum of the energy
delivered to all resistors).The product of current and resistance is taken as
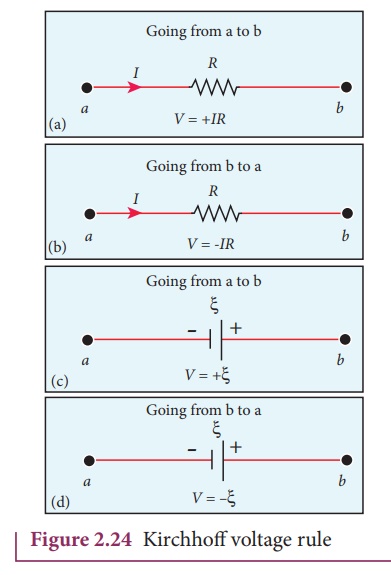
positive when the direction of the current is followed. Suppose if the
direction of current is opposite to the direction of the loop, then product of
current and voltage across the resistor is negative. It is shown in Figure 2.24
(a) and (b). The emf is considered positive when proceeding from the negative
to the positive terminal of the cell. It is shown in Figure 2.24 (c) and (d).
Kirchhoff voltage rule
has to be applied only when all currents in the circuit reach a steady state
condition (the current in various branches are constant).
EXAMPLE 2.21
The following figure
shows a complex network of conductors which can be divided into two closed
loops like ACE and ABC. Apply KirchoffŌĆÖs voltage rule.

Solution
Thus applying KirchoffŌĆÖs second law to the closed loop EACE
I1R1 + I2R2 + I3R3 = ╬Š
and for the closed loop ABCA
I4R4 + I5R5-I2R2= 0
EXAMPLE 2.22
Calculate
the current that flows in the 1ŌĆå╬® resistor in the following circuit.

Solution

We can
denote the current that flows from 9V battery as I1 and it splits
into I2 and I1 ŌĆō I2
in the junction according KirchoffŌĆÖs current rule (KCR). It is shown below.
Now consider the loop EFCBE and apply KVR, we get
1I2
+ 3I1 + 2I1 = 9
5I1 + I2 = 9 (1)
Applying KVR to the loop EADFE, we get
3 (I1
ŌĆō I2 ) ŌĆō 1I2 = 6
3I1
ŌĆō 4I2 = 6 (2)
Solving
equation (1) and (2), we get
I1
= 1.83 A and I2 = -0.13 A
It
implies that the current in the 1 ohm resistor flows from F to E.
Related Topics