Meaning of Derivatives | Mathematics - Derivative as rate of change | 12th Maths : UNIT 7 : Applications of Differential Calculus
Chapter: 12th Maths : UNIT 7 : Applications of Differential Calculus
Derivative as rate of change
Derivative as rate
of change
We have
seen how the derivative is used to determine slope. The derivative can also be
used to determine the rate of change of one variable with respect to another. A
few examples are population growth rates, production rates, water flow rates,
velocity, and acceleration.
A common
use of rate of change is to describe the motion of an object moving in a
straight line. In such problems, it is customary to use either a horizontal or
a vertical line with a designated origin to represent the line of motion. On
such lines, movements in the forward direction considered to be in the positive
direction and movements in the backward direction is considered to be in the
negative direction.
The
function s(t) that gives the position (relative to the origin) of an object as
a function of time t is called a
position function. It is denoted by s = f (t
) . The velocity and the
acceleration at time t is denoted as v(t) = ds/dt and a(t) = dv/dt = d2s/dt2
Remark
The
following remarks are easy to observe:
(i) Speed
is the absolute value of velocity regardless of direction and hence, Speed =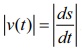 
(ii) • When the particle is at rest then v (t)
=
0.
• When the particle is moving forward then v (t)
>
0.
• When the particle is moving backward then v (t)
<
0.
• When the particle changes direction, v (t) then changes its
sign.
(iii) If
tc is the time point
between the time points t1
and t2 (t1 <
t c
<
t2 ) where the particle
changes direction then the total distance travelled from time t1 to time t2 is calculated as |s
(t1) − s(tc)| + |s(tc) − s(t2)|.
(iv) Near
the surface of the planet Earth, all bodies fall with the same constant
acceleration. When air resistance is absent or insignificant and only force acting
on a falling body is the force of gravity, we call the way the body falls is a
free fall.
An
object thrown at time t =
0 from initial height s0 with
initial velocity v0
satisfies the equation.
a = − g,
v = −gt + v0 , s = − gt2/2 + v0t + s0.
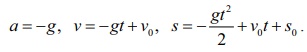
where, g = 9.8 m / s2 or 32 ft / s2 .
A few
examples of quantities
which are the rates
of change with respect to some other quantity in our daily life are given below:
1. Slope
is the rate
of change in vertical length with respect to horizontal length.
2. Velocity
is the rate
of displacement with respect to time.
3. Acceleration
is the rate
of change in velocity with respect to time.
4. The
steepness of a hillside is the rate of change in its elevation with respect to linear
distance.
Consider
the following two situations:
• A
person is continuously driving a car from Chennai to Dharmapuri. The distance
(measured in kilometre) travelled is expressed as a function of time (measured
in hours) by D (t) . What is the meaning one can attribute to D′(3) = 70 ?
It means
that, “the
rate of distance when t
= 3
is 70 kmph”.
• A
water source is draining with respect to the time t . The amount of water so drained after t days is expressed as V (t)
. What is the meaning of the slope of the tangent to the curve y = V (t) at
t = 7 is −3
?
It means
that, “the
water is draining at the rate of 3 units per day on day 7”.
Likewise
the rate of change concept can be used in our daily life problems. Let us now
illustrate this with more examples.
Example 7.2
The
temperature T in celsius in a long
rod of length 10 m, insulated at both ends, is a function of length x given by T = x(10 −
x) . Prove that the rate of change of
temperature at the midpoint of the rod is zero.
Solution
We are
given that, T =
10x − x2.
Hence, the rate of change at any distance from one end is given by dT/dx = 10 − 2x . The mid point of the rod is at x = 5 . Substituting x
=
5 , we get dT/dx =
0 .
Example 7.3
A person
learnt 100 words for an English test. The number of words the person remembers
in t days after learning is given by W (t)
=
100 ×
(1 −
0.1t)2 , 0 ≤
t ≤ 10 . What is the rate at which the
person forgets the words 2 days after learning?
Solution
We have,
d/dt W (t) = −20 × (1− 0.1t)
.
Therefore
at t = 2, d/dt W (t) = −16.
That is,
the person forgets at the rate of 16 words after 2 days of studying.
Example 7.4
A
particle moves so that the distance moved is according to the law s (t)
= t3/3
+ t2
+ 3 . At what time the velocity and acceleration are zero.
Solution
Distance
moved in time 't' is s = t3/3
− t2 + 3.
Velocity
at time 't ' is v (t) = ds/dt = t2 − 2t .
Acceleration
at time 't ' is a(t) = dV/dt = 2t − 2 .
Therefore,
the velocity is zero when t2
−
2t = 0 , that is t = 0, 2 . The acceleration is zero when 2t − 2 = 0 . That is at time t = 1.
Example 7.5
A
particle is fired straight up from the ground to reach a height of s feet in t seconds,where s(t)
= 128t −16t 2 .
(i) Compute
the maximum height of the particle reached.
(ii) What
is the velocity when the particle hits the ground?
Solution
(i) At
the maximum height, the velocity v(t) of the particle is zero.
Now, we
find the velocity of the particle at time t
.
v (t ) = ds/dt
= 128 − 32t
v (t) = 0
⇒ 128 − 32t = 0 ⇒ t = 4 .
After 4
seconds, the particle reaches the maximum height.
The
height at t =
4 is s(4) =
128(4) −16(4)2
=
256 ft.
(ii) When
the particle hits the ground then s =
0 .
s = 0 ⇒128t − 16t 2 = 0
⇒ t = 0, 8 seconds.
The
particle hits the ground at t =
8 seconds. The velocity when it hits the ground is v(8) = –128 ft /s.
Example 7.6
A
particle moves along a horizontal line such that its position at any time t ≥ 0 is given by s (t) = t3 − 6t2 + 9t +1 , where s is measured in metres and
t in seconds?
(i) At
what time the particle is at rest?
(ii) At
what time the particle changes its direction?
(iii) Find
the total distance travelled by the particle in the first 2 seconds.
Solution
Given
that s (t) = t3
−
6t2 +
9t +1 . On differentiating, we get v (t)
=
3t2 −12t +9 and a (t) =
6t −12.
(i) The
particle is at rest when v (t) = 0 . Therefore, v (t) =
3(t −1)(t − 3) = 0 gives t = 1and t =
3 .
(ii) The
particle changes its direction when v
(t) changes its sign. Now.
if 0 ≤
t < 1 then both (t −1) and (t −
3) <
0 and hence, v (t) > 0 .
If 1 <
t < 3 then (t − 1) > 0 and (t − 3) < 0 and hence, v (t) <
0 .
If t > 3 then both (t −1) and (t −
3) >
0 and hence, v (t) > 0 .
Therefore,
the particle changes its direction when t
=
1 and t =
3 .
(iii) The
total distance travelled by the particle from time t = 0 to t =
2 is given by, |s (0) – s(1) | + | s (1) − s(2) | =|1− 5 | + | 5 − 3 | = 6 metres.
Related Topics