Universal Law of Gravitation

Universal Law of Gravitation

Even though Kepler’s laws were able to explain the planetary motion, they failed to explain the forces responsible for it. It was Isaac Newton who analyzed Kepler’s laws, Galileo’s observations and deduced the law of gravitation.

Newton’s law of gravitation states that a particle of mass M₁ attracts any other particle of mass M₂ in the universe with an attractive force. The strength of this force of attraction was found to be directly proportional to the product of their masses and is inversely proportional to the square of the distance between them. In mathematical form, it can be written as:

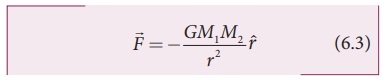
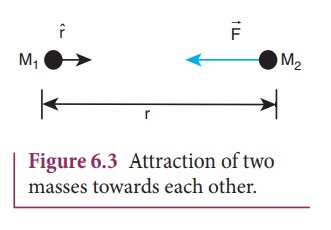
Where  is the unit vector from M₁ towards M₂ as shown in Figure 6.3, and G is the Gravitational constant that has the value of 6.626 × 10^−11 N m² kg^−2 , and r is the distance between the two masses M₁ and M₂ . In Figure 6.3, the vector  denotes the gravitational force experienced by M₂ due to M₁ . Here the negative sign indicates that the gravitational force is always attractive in nature and the direction of the force is along the line joining the two masses.

In  cartesian  coordinates,  the  square of the distance is expressed as y r ² = (x² + ² z²). This is dealt in unit 2.

EXAMPLE 6.1

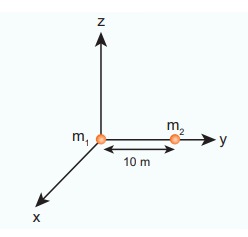
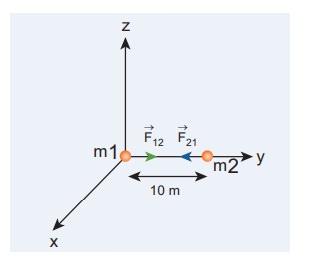
Consider two point masses m₁ and m₂ which are separated by a distance of 10 meter as shown in the following figure. Calculate the force of attraction between them and draw the directions of forces on each of them. Take m₁= 1 kg and m₂ = 2 kg

Solution

The force of attraction is given by

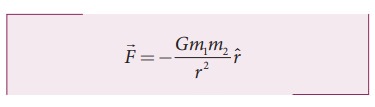
From the figure, r =10 m.

First, we can calculate the magnitude of the force

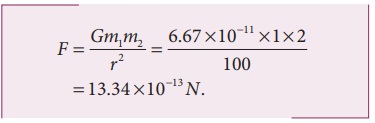
It is to be noted that this force is very small. This is the reason we do not feel the gravitational force of attraction between each other. The small value of G plays a very crucial role in deciding the strength of the force.

The force of attraction () experienced by the mass m₂ due to m₁ is in the negative ‘y’ direction ie., rˆ =−jˆ . According to Newton’s third law, the mass m₂ also exerts equal and opposite force on m₁. So the force of attraction () experienced by m₁ due to m₂ is in the direction of positive ‘y’ axis ie., rˆ = jˆ .

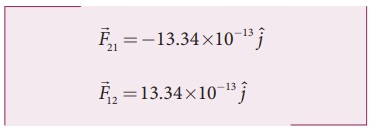
The direction of the force is shown in the figure,

Gravitational force of attraction between m₁ and m₂

= − which confirms Newton’s third law.

Important features of gravitational force:

As the distance between two masses increases, the strength of the force tends to decrease because of inverse dependence on r². Physically it implies that the planet Uranus experiences less gravitational force from the Sun than the Earth since Uranus is at larger distance from the Sun compared to the Earth.

The gravitational forces between two particles always constitute an action-reaction pair. It implies that the gravitational force exerted by the Sun on the Earth is always towards the Sun. The reaction-force is exerted by the Earth on the Sun. The direction of this reaction force is towards Earth.

The torque experienced by the Earth due to the gravitational force of the Sun is given by

It implies that angular momentum  is a constant vector. The angular momentum of the Earth about the Sun is constant throughout the motion. It is true for all the planets. In fact, this constancy of angular momentum leads to the Kepler’s second law.

The expression 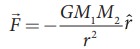 has one inherent assumption that both M₁  and M₂ are treated as point masses. When it is said that Earth orbits around the Sun due to Sun’s gravitational force, we assumed Earth and Sun to be point masses. This assumption is a good approximation because the distance between the two bodies is very much larger than their diameters. For some irregular and extended objects separated by a small distance, we cannot directly use the equation (6.3). Instead, we have to invoke separate mathematical treatment which will be brought forth in higher classes.

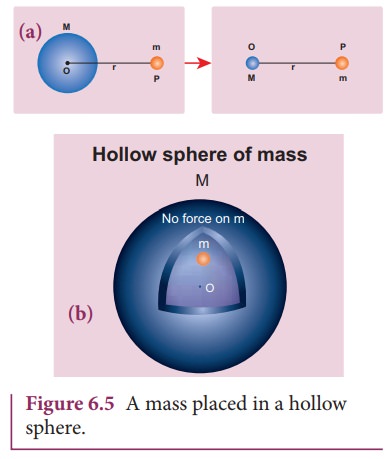
However, this assumption about point masses holds even for small distance for one special case. To calculate force of attraction between a hollow sphere of mass M with uniform density and point mass m kept outside the hollow sphere, we can replace the hollow sphere of mass M as equivalent to a point mass M located at the center of the hollow sphere. The force of attraction between the hollow sphere of mass M and point mass m can be calculated by treating the hollow sphere also as another point mass. 

Essentially the entire mass of the hollow sphere appears to be concentrated at the center of the hollow sphere. It is shown in the Figure 6.5(a).

There is also another interesting result. Consider a hollow sphere of mass M. If we place another object of mass ‘m’ inside this hollow sphere as in Figure 6.5(b), the force experienced by this mass ‘m’ will be zero. This calculation will be dealt with in higher classes.

The triumph of the law of gravitation is that it concludes that the mango that is falling down and the Moon orbiting the Earth are due to the same gravitational force.

Newton’s inverse square Law:

Newton considered the orbits of the planets as circular. For circular orbit of radius r, the centripetal acceleration towards the center is

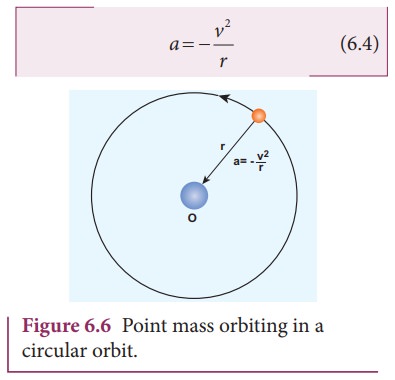
Here v is the velocity and r, the distance of the planet from the center of the orbit (Figure 6.6).

The velocity in terms of known quantities r and T, is

Here T is the time period of revolution of the planet. Substituting this value of v in equation (6.4) we get,

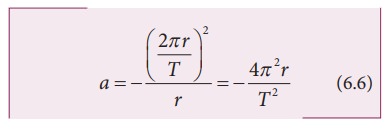
Substituting the value of ‘a’ from (6.6) in Newton’s second law, F = ma, where ‘m’ is the mass of the planet.

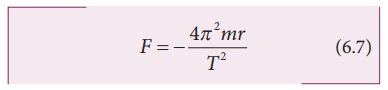
From Kepler’s third law,

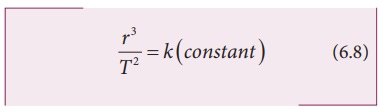
By substituting equation 6.9 in the force expression, we can arrive at the law of gravitation.

Here negative sign implies that the force is attractive and it acts towards the center. In equation (6.10), mass of the planet ‘m’ comes explicitly. But Newton strongly felt that according to his third law, if Earth is attracted by the Sun, then the Sun must also be attracted by the Earth with the same magnitude of force. So he felt that the Sun’s mass (M) should also occur explicitly in the expression for force (6.10). From this insight, he equated the constant 4Ï€²k to GM which turned out to be the law of gravitation

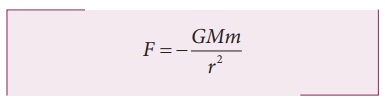
Again the negative sign in the above equation implies that the gravitational force is attractive.

In the above discussion we assumed that the orbit of the planet to be circular which is not true as the orbit of the planet around the Sun is elliptical. But this circular orbit assumption is justifiable because planet’s orbit is very close to being circular and there is only a very small deviation from the circular shape.

EXAMPLE 6.2

Moon and an apple are accelerated by the same gravitational force due to Earth. Compare the acceleration of the two.

The gravitational force experienced by the apple due to Earth

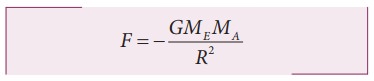
Here M_A – Mass of the apple, M_E– Mass of the Earth and R – Radius of the Earth.

Equating the above equation with Newton’s second law,

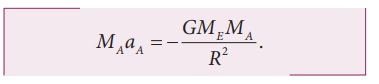
Simplifying the above equation we get,

Here a_A is the acceleration of apple that is equal to ‘g’.

Similarly the force experienced by Moon due to Earth is given by

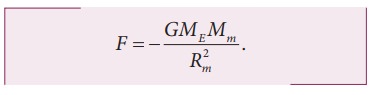
Here R_m- distance of the Moon from the Earth, M_m – Mass of the Moon

The acceleration experienced by the Moon is given by

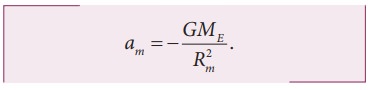
The ratio between the apple’s acceleration to Moon’s acceleration is given by

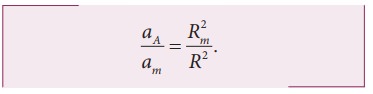
From the Hipparchrus measurement, the distance to the Moon is 60 times that of Earth radius. R_m = 60R.

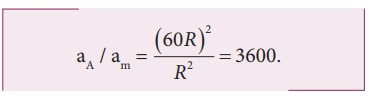
The apple’s acceleration is 3600 times the acceleration of the Moon.

The same result was obtained by Newton using his gravitational formula. The apple’s acceleration is measured easily and it is 9.8 m s^−2 . Moon orbits the Earth once in 27.3 days and by using the centripetal acceleration formula, (Refer unit 3).

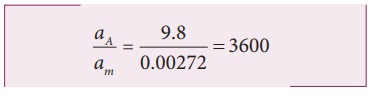
which is exactly what he got through his law of gravitation.