Gravitational field

Gravitational field

Force is basically due to the interaction between two particles. Depending upon the type of interaction we can have two kinds of forces: Contact forces and Non-contact forces (Figure 6.8).

Contact forces are the forces applied where one object is in physical contact with the other. The movement of the object is caused by the physical force exerted through the contact between the object and the agent which exerts force.

Consider the case of Earth orbiting around the Sun. 

Though the Sun and the Earth are not physically in contact with each other, there exists an interaction between them. This is because of the fact that the Earth experiences the gravitational force of the Sun. This gravitational force is a non-contact force.

It sounds mysterious that the Sun attracts the Earth despite being very far from it and without touching it. For contact forces like push or pull, we can calculate the strength of the force since we can feel or see. But how do we calculate the strength of non-contact force at different distances? To understand and calculate the strength of non-contact forces, the concept of ‘field’ is introduced.

The gravitational force on a particle of mass ‘m₂’ due to a particle of mass ‘m₁’ is

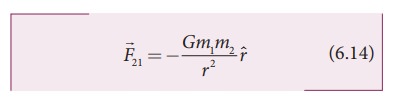
Where rˆ  is a unit vector that points from m₁ to m₂ along the line joining the masses m₁ and m₂.

The gravitational field intensity  (here after called as gravitational field) at a point which is at a distance r from m₁ is defined as the gravitational force experienced by unit mass placed at that point. It is given by the ratio  /m₂ (where m₂ is the mass of the object m₂ on which  acts)

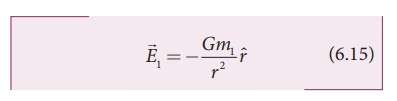
Using =  /m2 in equation (6.14) we get, is a vector quantity that points towards the mass m₁ and is independent of mass m₂, Here m₂ is taken to be of unit magnitude . The unit rˆ is along the line between m₁ and the point in question. The field  is due to the mass m₁.

In general, the gravitational field intensity due to a mass M at a distance r is given by

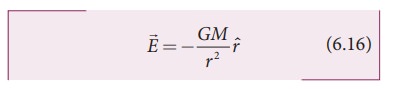
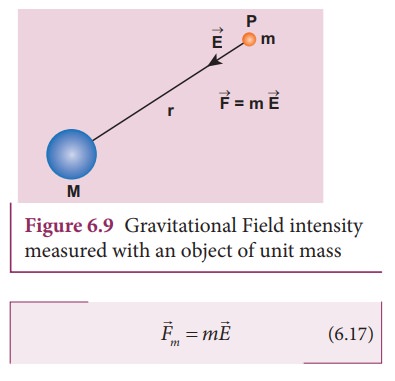
Now in the region of this gravitational field, a mass ‘m’ is placed at a point P (Figure 6.9). Mass ‘m’ interacts with the field  and experiences an attractive force due to M as shown in Figure 6.9. The gravitational force experienced by ‘m’ due to ‘M’ is given by

Now we can equate this with Newton’s second law 

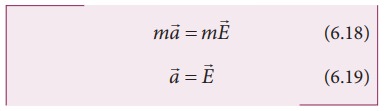
In other words, equation (6.18) implies that the gravitational field at a point is equivalent to the acceleration experienced by a particle at that point. However, it is to be noted that  and  are separate physical quantities that have the same magnitude and direction. The gravitational field  is the property of the source and acceleration  is the effect experienced by the test mass (unit mass) which is placed in the gravitational field . The non-contact interaction between two masses can now be explained using the concept of “Gravitational field”.

Points to be noted:

i) The strength of the gravitational field decreases as we move away from the mass M as depicted in the Figure 6.10. The magnitude of  decreases as the distance r increases.

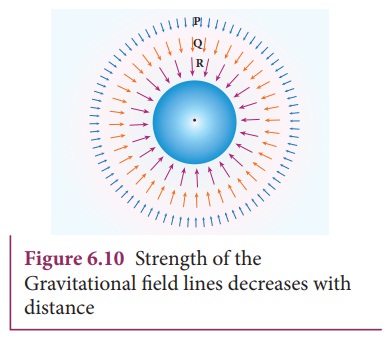
Figure 6.10 shows that the strength of the gravitational field at points P, Q, and R is given by . It can be understood by comparing the length of the vectors at points P, Q, and R.

ii) The “field” concept was introduced as a mathematical tool to calculate gravitational interaction. Later it was found that field is a real physical quantity and it carries energy and momentum in space. The concept of field is inevitable in understanding the behavior of charges.

iii) The unit of gravitational field is Newton per kilogram (N/kg) or m s^-2.