Gravitation | Physics - Long Questions and Answer | 11th Physics : UNIT 6 : Gravitation
Chapter: 11th Physics : UNIT 6 : Gravitation
Long Questions and Answer
Gravitation (Physics)
Long
Answer Questions
1.
Discuss the important features of the law of gravitation.
Important
features of gravitational force:
ŌŚÅ
As the distance between two masses increases, the strength of the force tends
to decrease because of inverse depends on r2.
ŌŚÅ
Uranus experiences less gravitational force from the Sun than the Earth since
Uranus is at larger distance from the Sun compared to Earth.
ŌŚÅ
The gravitational forces between two particles always constitute an action
reaction pair.
ŌŚÅ
The gravitational force exerted by the Sun on the Earth is always towards the
Sun.
ŌŚÅ
The reaction- force is exerted by the sun on the Earth on the Sun.
ŌŚÅ
The direction of this reaction force is towards Earth.
ŌŚÅ The torque experienced by angular momentum is a constant vector.
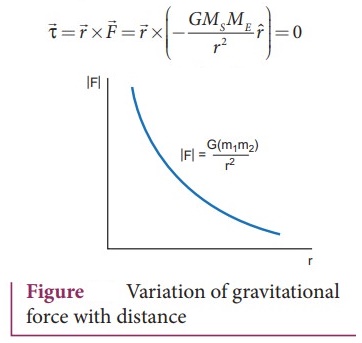
ŌŚÅ
The angular momentum of the Earth about the Sun is constant throughout the
motion
ŌŚÅ
Earth orbits around the Sun due to Sun's gravitational force,
ŌŚÅ
To calculate force of attraction between hollow sphere of mass M with uniform
density and point mass m kept outside the hollow sphere, we can replace the
hollow sphere of mass M as equivalent to a point mass M located at the centre
of the hollow sphere.
ŌŚÅ
If we place another object of mass 'm' inside this hollow sphere, the force
experiencedby this mass 'm' will be zero.
2.
Explain how Newton arrived at his law of gravitation from KeplerŌĆÖs third law.
NewtonŌĆÖs inverse square Law:
Newton
considered the orbits of the planets as circular. For circular orbit of radius
r, the centripetal acceleration towards the centre is
a
= - v2 / r ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”(1)
Here
v is the velocity and r, the distance of the planet from the centre of the
orbit. The velocity in terms of known quantities r and T, is
v
= 2ŽĆr / T ŌĆ”ŌĆ”ŌĆ”ŌĆ” (2)
Here
T is the time period of revolution of the planet. Substituting this value of v
in equation (1) we get.
a
= (2ŽĆr / T)2 / r = ŌłÆ 4ŽĆ2r / T2 ŌĆ”ŌĆ”.. (3)
Substituting
the value of ŌĆśaŌĆÖ from (3) in Newton's second law, F=ma, where ŌĆśm' is the mass
of the planet.
F=
ŌłÆ 4ŽĆ2mr / T2
ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(4)
From
Kepler's third law
r3/
T2 = K (constant) ŌĆ”ŌĆ”ŌĆ”.(5)
r
/ T2 = K /r2 ŌĆ”ŌĆ”ŌĆ”.(6)
By
substituting equation 6 in the force expression, we can arrive at the law of
gravitation.
F=
ŌłÆ 4ŽĆ2mK / r2 ŌĆ”ŌĆ”ŌĆ”.(7)
ŌŚÅ
Negative sign implies that the force is attractive and it acts towards the
centre.
ŌŚÅ
According to Newtons third law, if Earth is attracted by the Sun, then the Sun
must also be attracted by the Earth with the same magnitude of force.
ŌŚÅ
The Sun's mass (M) should also occur explicitly in the expression for force.
ŌŚÅ
From this insight, he equated the constant to GM which turned out to be law of
gravitation.
F
= ŌłÆ GMm / r2
The
negative sign implies that the gravitational force is attractive.
3.
Explain how Newton verified his law of gravitation.
ŌŚÅ
Newton verified his law of universal gravitation by comparing the acceleration
of a terrestrial object to the acceleration of the moon.
ŌŚÅ
He knew that the distance from the centre of earth to the centre of two spheres
of known mass at either end of a light rod suspended by a thin fibre from the
centre of the rod.
ŌŚÅ
He found earlier that the small force that was needed to twist the fibre.
ŌŚÅ
By bringing a third sphere close to one of the suspended spheres.
ŌŚÅ
He was able to measure the force of gravity between the spheres and hence
gravitation.
4. Derive the expression for gravitational potential energy.
ŌŚÅ
Among the two masses, m1 to be fixed in its position, work must be
done on m2 to move the distance from rŌĆÖ to r.
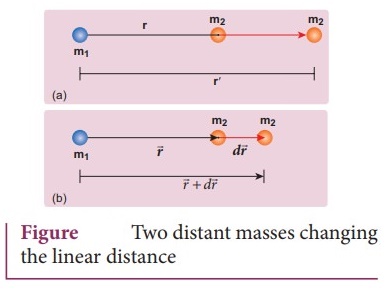
Two
distant masses changing the linear distance
ŌŚÅ
To move the mass m2 through an infinitesimal displacement d![]() from
from ![]() to
to ![]() + d
+ d![]() , work has to be done externally. This infinitesimal work
is given by
, work has to be done externally. This infinitesimal work
is given by 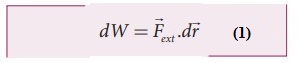 ŌĆ”ŌĆ”ŌĆ”(1)
ŌĆ”ŌĆ”ŌĆ”(1)
ŌŚÅ
The work is done against gravitational force, therefore,

Substituting
Equation (2) in (1), we get

Ōł┤ dW = [ Gm1m2
/ r2 ] dr ŌĆ”ŌĆ”ŌĆ”ŌĆ”. (5)
Thus
the total work done for displacing the particle from r' to r is
W = ╩ārrŌĆÖdW
= ╩ārrŌĆÖ [
Gm1m2 / r2 ]
dr
W = ŌłÆ (Gm1m2
/ r) rrŌĆÖ
W = ŌłÆ [ Gm1m2
/ r ] + [ Gm1m2 / r' ]
W = U(r) - U(r')
where
U(r) = [ŌłÆGm1m2 ] / r

This
work done W gives the gravitational potential energy difference of the system
of masses m1 and m2 when the separation between them are
r and r' respectively
Case
1:
If r < r'
Since
gravitational force is attractive, m2 is attracted by m1.
Then m2 can move from r' to r without any external work. Here work
is done by the system spending its internal energy and hence the work done is
said to be negative.
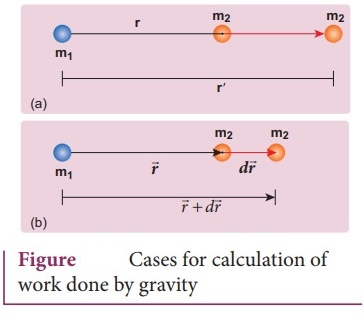
Case
2:
If r>r'
ŌŚÅ
Work has to be done against gravity to move the object from r' to r. Therefore
work is done on the body by external force and hence work done is positive.
ŌŚÅ
Now gravitational potential energy can be discussed by choosing one point as
the reference point.
ŌŚÅ
Let us choose r . Then the second term in the equation becomes zero.
W = ŌłÆ [ Gm1m2
/ r ] + 0

ŌŚÅ
Now we can define gravitational potential energy of a system of two masses m1
and m2 separated by a distance r as the amount of work done to take
the mass m2 from a distance r to infinity assuming m1 to
be fixed in its position and is written as U (r) = - [ Gm1m2
/ r ] when the masses are separated by an infinite distance and by
distance r. U (r) = U(r) ŌłÆ U (ŌłØ).
ŌŚÅ
Here we choose U(ŌłØ) = 0 as
the reference point.
ŌŚÅ
The gravitational potential energy U(r) is always negative.
ŌŚÅ The unit of gravitational potential energy U (r) is Joule and it is a scalar quantity.
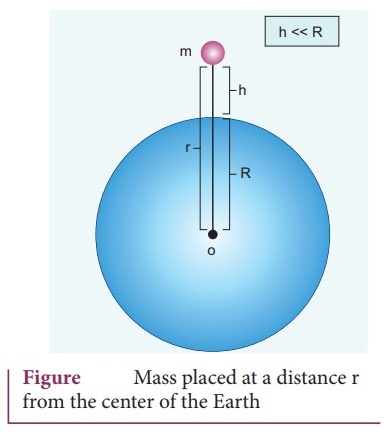
5.
Prove that at points near the surface of the Earth, the gravitational potential
energy of the object is U = mgh
ŌŚÅ
Consider the Earth and mass system, with r, the distance between the mass m and
the Earth's centre. Then the gravitational potential energy.
h<<R
U
= ŌłÆ [ GMem / r ] ŌĆ”ŌĆ”ŌĆ”.(1)
ŌŚÅ
r = Re + h Re is the radius of the Earth. h is the height
above the Earth's surface,
U
= ŌłÆ G [ Mem / (Re+h) ] ŌĆ”ŌĆ”ŌĆ”.(2)
If
h << Re, equation (2) can be modified as
U
= -G [ Mem / Re( 1+h / R )e ]
U
= ŌłÆ G [ Mem / Re ] ( 1+h / Re )ŌłÆ1 ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(3)
ŌŚÅ
Using Binomial expansion and neglecting the higher order terms, we get
U
= ŌłÆ G [ Mem / Re ] ( 1- h/Re) ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(4)
We
know that, for a mass m on the Earth's surface
G
[ Mem / Re ] = mgRe ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(5)
Substituting
equation (5) in (4) we get,
U
= ŌłÆ mgRe + mgh ŌĆ”ŌĆ”ŌĆ”ŌĆ”(6)
The
first term in the above expression is independent of the height h. For example,
if the object is taken from height h1 to h2, then the
potential energy at h1 is
U(h1)
= ŌłÆmgRe + mgh1 ŌĆ”ŌĆ”ŌĆ”ŌĆ” (7)
and
the potential energy at h2 is
U(h2)
= ŌłÆmgRe + mgh2 ŌĆ”ŌĆ”ŌĆ”ŌĆ” (8)
The
potential energy difference between hl (doubt)and h2 is
U(h2)
ŌłÆ U(h1) = mg (h2 ŌłÆ h1) . ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. (9)
Omitting
the first term (1) and (2) we get.
U
= mgh
6.
Explain in detail the idea of weightlessness using lift as an example.
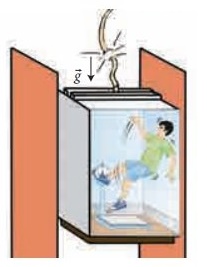
ŌŚÅ
When the lift falls (when the lift wire cuts) with downward acceleration a=g,
then person inside the elevator is in state of weightlessness or free fall.
ŌŚÅ
As they fall freely, they are not in contact with any surface (by neglecting air
friction).
ŌŚÅ
The normal force acting on the object is zero.
ŌŚÅ
The downward acceleration is equal to the acceleration due to the gravity of
the Earth.
i.e (a=g).
From equation N=m (g-a) we get,
a
= g
Ōł┤ N = m
(g-g) = 0.
This
is called the state of weightlessness.
7.
Derive an expression for escape speed.
ŌŚÅ
Consider an object of mass M on the surface of the Earth. When it is thrown up
with an initial speed vi, the initial total energy of the object is
Ei
= 1/2 MVi 2 ŌĆō [ GMME / RE ] ŌĆ”ŌĆ”ŌĆ”. (1)
Where
ME, is the mass of the Earth and RE -the radius of the
Earth.
The
term ŌłÆGMME / RE is the potential energy of the mass M.ŌĆā
ŌŚÅ
When the object reaches a height far away from Earth and hence treated as
approaching infinity, the gravitational potential energy becomes zero [U(Ōł×)=0]
and the kinetic energy becomes zero as well.
ŌŚÅ
Therefore the final total energy of the object becomes zero.
ŌŚÅ
This is for minimum energy and for minimum speed to escape. Otherwise kinetic
energy can be non- zero.
Ef
= 0, According to the law of energy conservation,
Ei
= Ef ŌĆ”ŌĆ”ŌĆ”ŌĆ”. (2)
Substituting
(1) in (2) we get.
1/2
MVi 2 ŌłÆ GMME /RE = 0
1/2
MVi 2 ŌłÆ GMME /RE ŌĆ”ŌĆ”ŌĆ”ŌĆ”(3)
ŌŚÅ
The escape speed, the minimum speed required by an object to escape from
Earth's gravitational field, replacing,
vi with ve.
i.e
1/2
MVe 2 = GMME / RE
Ve 2 = ŌłÆ GMME
/ RE . 2/M
Ve 2 = - 2GME
/ RE ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”..(4)
Using
g = GME / R2E ,
Ve2 = 2gRE
Ve = ŌłÜ[2gRE] ŌĆ”ŌĆ”ŌĆ”ŌĆ”.. (5)
From
equation (5) the escape speed depends on two factors: acceleration due to
gravity and radius of the Earth. It is completely independent of the mass of
the object.
8.
Explain the variation of g with lattitude.
Variation
of g with latitude:
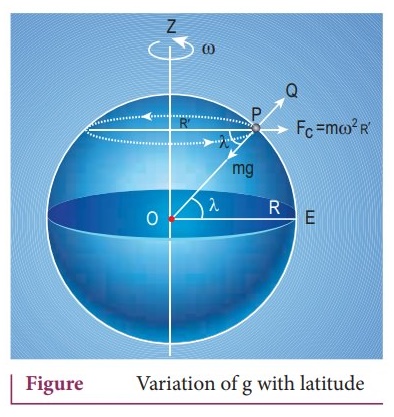
ŌŚÅ
Whenever we analyze the motion of objects in rotating frames, we must taken
into account the centrifugal force.
ŌŚÅ
Even though the Earth is an inertial frame, it is not exactly correct because
the Earth spins about its own axis.
ŌŚÅ
So when an object is on the surface of the Earth, it experiences a centrifugal
force that depends on the latitude of the object on Earth. If the Earth were
not spinning, the force on the object would have been mg. However, the object
experiences an additional centrifugal force due to spinning of the Earth.
ŌŚÅ
This centrifugal force is given by mŽēRR'
R'
= R cos ╬╗ ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”. (1)
Where
╬╗ is the latitude. The component of centrifugal acceleration experienced by the
object in the direction opposite to g is
ac
= Žē2R' cos ╬╗ = Žē2R cos2 ╬╗ since R' cos ╬╗
Therefore,
g' = g ŌłÆ Žē2R cos2 ╬╗ ŌĆ”ŌĆ”ŌĆ”. (2)
From
the expression (2). At equator, ╬╗ = 0; g' = g ŌłÆ Žē2R. The
acceleration due to gravity is minimum. At poles g' = g, it is maximum. At the
equator, g' minimum.
9.
Explain the variation of g with altitude.
Variation of g with altitude:
Consider
an object of mass m at a height h from the surface of the Earth.
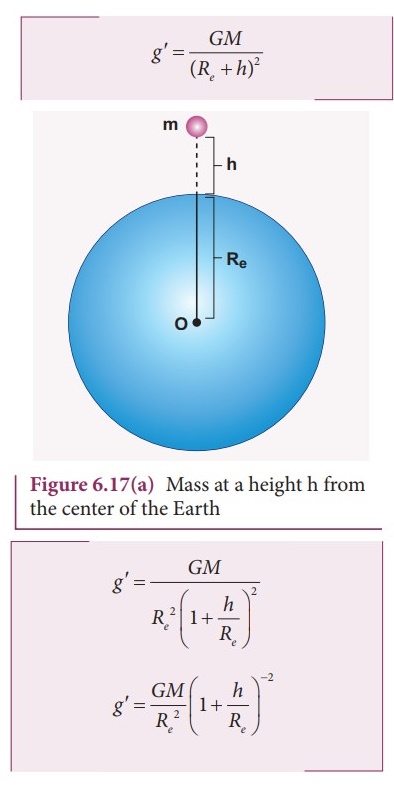
Acceleration
experienced by the object due to Earth is
g' = GM / (Re
+ h)2

If
h << Re Using Binomial expansion, taking the terms upto first
order

g' < g.
As altitude h increase, the acceleration due to gravity g decreases.
10.
Explain the variation of g with depth from the EarthŌĆÖs surface.
Variation
of g with depth:

Consider
a particle of mass m which is in a deep mine on the earth. Ex. Coal mines -
Neyveli). Assume the depth of the mine as d. The part of the Earth which is
above the radius (Re-d) do not contribute to the acceleration.
g' = GM'/ (Re
ŌĆō d)2 Here M is the mass of the Earth and radius (Re-d).
Assuming the density of earth to be constant,
p
=
M' / V' ; M' / V' = M / V and M' = [M / V] V'

g'
< g As depth increases, decreases.
11.
Derive the time period of satellite orbiting the Earth.
Time
period of the satellite:
ŌŚÅ
The distance covered by the satellite during one rotation in its orbit is equal
to 2ŽĆ(RE+h) and time taken for it is the time period. T. Then
v = Distance
travelled / Time taken = 2ŽĆ (RE+h) / T
From
equation,

Squaring both side, of the equation (2), we get T2= 4ŽĆ2 /GME (RE+h)3
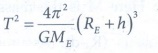
4ŽĆ2
/GME = Constant say c, T2=c(RE+h)3 ŌĆ”ŌĆ”ŌĆ”
(3)
ŌŚÅ
Equation (3) implies that a satellite orbiting the Earth has the same relation
between time and distance as that of Kepler's law of planetary motion. For a
satellite orbiting near the surface of the Earth, h is negligible compared to
the radius of the Earth RE.
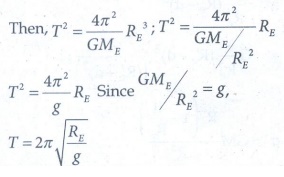
T = 2 ŽĆ
ŌłÜ[RE /g]
12.
Derive an expression for energy of satellite.
ŌŚÅ
The total energy of a satellite orbiting the Earth at a distance h from the
surface of Earth
ŌŚÅ
The total energy of the satellite is the sum of its kinetic energy and the
gravitational potential energy.
ŌŚÅ
The potential energy of the satellite is,
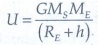
U
=
GMSME / (RE+h) ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”.(1)
MS
- mass of the satellite,
ME
- mass of the Earth,
RE
-radius of the Earth.
ŌŚÅ
The kinetic energy of the satellite is
KE
= 1/2 MS v2 ŌĆ”ŌĆ”ŌĆ”. (2)
v is the
orbital speed of the satellite is equal to v = ŌłÜ [ GME /
(RE+h) ]
ŌŚÅ
Substituting the value of v in (2), the kinetic energy of the satellite
becomes,
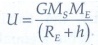
ŌŚÅ
Therefore the total energy of the satellite is
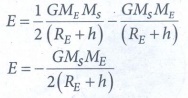
ŌŚÅ
The negative sign in the total energy implies that the satellite is bound to
the Earth and it cannot escape from the Earth.
13.
Explain in detail the geostationary and polar satellites.
Geo-stationary
and polar satellite
ŌŚÅ
The satellites orbiting the Earth have different time periods corresponding to
different orbital radii.
ŌŚÅ
Kepler's third law is used to find the radius of the orbit.
T2 = (4ŽĆ2/GME
)(RE + h)3
(RE
+ h)3 = GME T2 / 4ŽĆ2
RE
+ h = (GME T2 / 4ŽĆ2)1/3

ŌŚÅ
Substituting for the time period (24 hrs= 86400 seconds), mass and radius of
the Earth, h turns out to be 36,000 km. Such satellites are called "geo-stationary
satellites", since they appear to be stationary when seen from Earth.
ŌŚÅ
Geo-stationary satellite for the purpose of telecommunication. Another type of
satellite which is placed at distance of 500 to 800 km from the surface of the
Earth orbits the Earth from north to south direction.
ŌŚÅ
This type of satellite use that orbits Earth from North pole to South pole is
called a polar satellite. The time period of a polar satellite is nearly 100
minutes and the satellite completes many revolutions in a day.
ŌŚÅ
A Polar satellite covers a small strip of area pole to pole during one
revolution. In the next revolution it covers a different strip of area since
the Earth would have moved by a small angle.
14. Explain how geocentric theory is replaced by heliocentric theory using the idea of retrograde motion of planets.
ŌŚÅ
Ptolemy introduced the concept of "epicycle" in his geocentric model.
According to this theory, while the planet orbited the Earth, it also underwent
another circular motion termed as "epicycle".
ŌŚÅ
A combination of epicycle and circular motion around the Earth gave rise to
retrograde motion of the planets with respect to Earth.
ŌŚÅ
But ptolemy's model became more and more complex as every planet was found to
undergo retrograde motion.
ŌŚÅ
According to Copernicus model, the Sun is at the centre of the solar system and
all planets orbited the Sun.
ŌŚÅ
The retrograde motion of planets with respect to Earth is because of the
relative motion of the planet with respect to Earth.
15.
Explain in detail the Eratosthenes method of finding the radius of Earth.
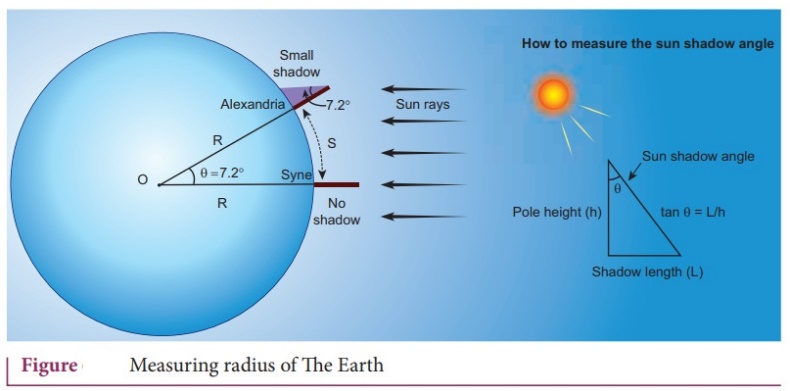
ŌŚÅ
During noon time of summer solstice the Sun's rays cast no shadow in the city
Syne which was located 500 miles away from Alexandria.
ŌŚÅ
At the same day and same time in Alexandria, the Sun's rays made 7.2 degree
with local vertical
ŌŚÅ
This difference of 7.2 degree was due to the curvature of the Earth.
ŌŚÅ
The angle 7.2 degree is equivalent to 1/8 radian. So, ╬Ė = 1/8 rad.
ŌŚÅ
If S is the length of the arc between the cities of Syne and Alexandria, and if
R is radius, then , S=R╬Ė=500 miles, so radius of the Earth
ŌŚÅ
R = 500 miles / (1/8)
R
= 4,000 miles
1
mile is equal to 1.609 km. The radius of the Earth to be equal to R=6436km,
which is amazingly close to the correct value of 6378 km.
16.
Describe the measurement of EarthŌĆÖs shadow (umbra) radius during total lunar
eclipse
ŌŚÅ
It is possible to measure the radius of shadow of the Earth at the point where
the Moon crosses.
ŌŚÅ
When the Moon is inside the umbra shadow, it appears red in color. As soon as
the Moon exist from the umbra shadow, it appears in crescent shape.
ŌŚÅ
By finding the apparent radii of the Earth's umbra shadow and the Moon, the
ratio of the these radii can be calculated.
ŌŚÅ
The apparent radius of Earth's umbra shadow = RS = 13.2 cm
ŌŚÅ
The apparent radius of the moon Rm = 5.15 cm
The
ratio Rs / Rm Ōēł 2.56.
The
radius of the Earth's umbra shadow is Rs = 2.56 ├Ś Rm
ŌŚÅ
The radius of Moon, Rm = 1737 km
ŌŚÅ
The radius of the Earth's umbra shadow is Rs = 2.56 ├Ś 1737 km ŌēĪ 4446
km
ŌŚÅ
The correct radius is 4610 km
ŌŚÅ
Percentage error = [ (4610 ŌĆō 4446) / 4610 ] ├Ś 100 = 35 %
The
error will be reduced if the pictures are taken using a high quality telescope.
Related Topics