Gravitational Potential Energy

Gravitational Potential Energy

The concept of potential energy and its physical meaning were dealt in unit 4. The gravitational force is a conservative force and hence we can define a gravitational potential energy associated with this conservative force field.

Two masses m₁ and m₂ are initially separated by a distance r′. Assuming m₁ to be fixed in its position, work must be done on m₂ to move the distance from r′ to r as shown in Figure 6.12(a)

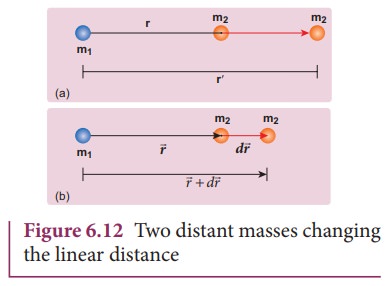
To move the mass m₂ through an infinitesimal displacement d from  to  + d (shown in the Figure 6.12(b)), work has to be done externally. This infinitesimal work is given by

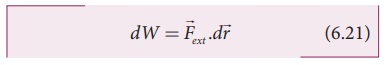
The work is done against the gravitational force, therefore,

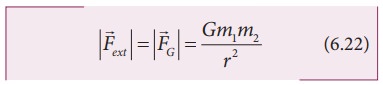
Substituting Equation (6.22) in 6.21, we get

Also we know,

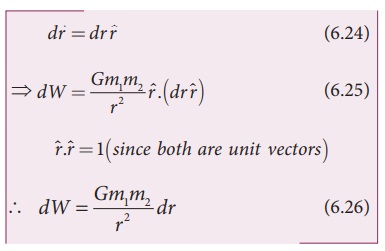
Thus the total work done for displacing the particle from r′ to r is

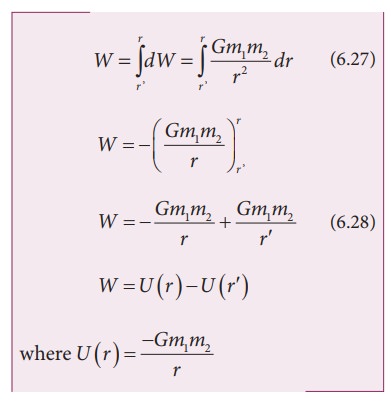
This work done W gives the gravitational potential energy difference of the system of masses m₁ and m₂ when the separation between them are r and r′ respectively.

Case 1: If r <r’

Since gravitational force is attractive, m₂ is attracted by m₁.Then m₂ can move from r to r′ without any external work (Figure 6.13). Here work is done by the system spending its internal energy and hence the work done is said to be negative.

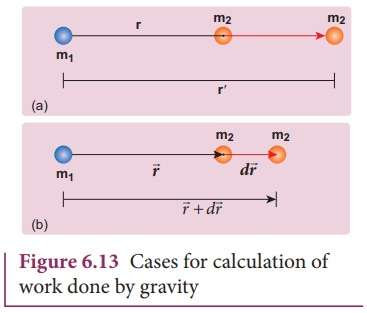
Case 2: If r > r′

Work has to be done against gravity to move the object from r′ to r. Therefore work is done on the body by external force and hence work done is positive.

It is to be noted that only potential energy difference has physical significance. Now gravitational potential energy can be discussed by choosing one point as the reference point.

Let us choose r’=∞ . Then the second term in the equation (6.28) becomes zero.

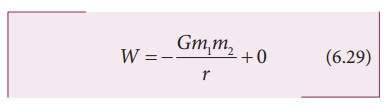
Now we can define gravitational potential energy of a system of two masses m₁ and m₂ separated by a distance r as the amount of work done to bring the mass m₂ from infinity to a distance r assuming m₁ to be fixed in its position and is written as

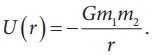
It is to be noted that the gravitational potential energy of the system consisting of two masses m1 and m2 separated by a distance r, is the gravitational potential energy difference of the system when the masses are separated by an infinite distance and by distance r. U ( r ) = U ( r ) - U ( ∞ ). Here we choose U  ( ∞ )= 0 as the reference point. The gravitational potential energy U( r ) is always negative because when two masses come together slowly from infinity, work is done by the system.

The unit of gravitational potential energy U ( r ) is Joule and it is a scalar quantity. The gravitational potential energy depends upon the two masses and the distance between them.