Energy of an Orbiting Satellite

Energy of an Orbiting Satellite

The total energy of a satellite orbiting the Earth at a distance h from the surface of Earth is calculated as follows; The total energy of the satellite is the sum of its kinetic energy and the gravitational potential energy. The potential energy of the satellite is,

Here Ms - mass of the satellite, ME - mass of the Earth, RE - radius of the Earth. The Kinetic energy of the satellite is

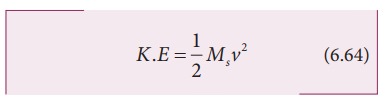
Here v is the orbital speed of the satellite and is equal to

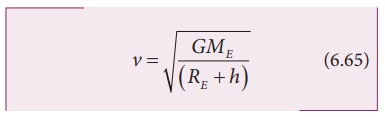
Substituting the value of v in (6.64), the kinetic energy of the satellite becomes,

The negative sign in the total energy implies that the satellite is bound to the Earth and it cannot escape from the Earth.

As h approaches ∞, the total energy tends to zero. Its physical meaning is that the satellite is completely free from the influence of Earth’s gravity and is not bound to Earth at large distances.

EXAMPLE 6.10

Calculate the energy of the (i) Moon orbiting the Earth and (ii) Earth orbiting the Sun.

Solution

Assuming the orbit of the Moon to be circular, the energy of Moon is given by,

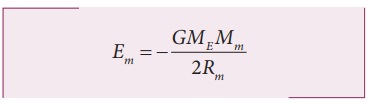
where  ME is the mass  of Earth 6.02 ×1024  kg; Mm is the mass of Moon 7.35 ×1022 kg; and R  is the distance between the Moon and the center of the Earth 3.84 ×105 km

The negative energy implies that the Moon is bound to the Earth.

Same method can be used to prove that the energy of the Earth is also negative.