Gravitational potential energy near the surface of the Earth

Gravitational potential energy near the surface of the Earth

It is already discussed in chapter 4 that when an object of mass m is raised to a height h, the potential energy stored in the object is mgh (Figure 6.14). This can be derived using the general expression for gravitational potential energy.

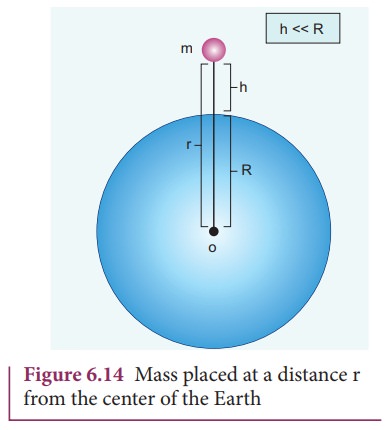
Consider the Earth and mass system, with r, the distance between the mass m and the Earth’s centre. Then the gravitational potential energy,

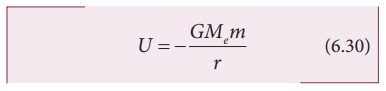
Here r = R_e+h, where R_e is the radius of the Earth. h is the height above the Earth’s surface

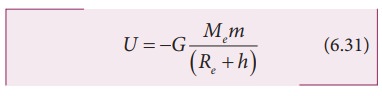
If h << R_e, equation (6.31) can be modified as

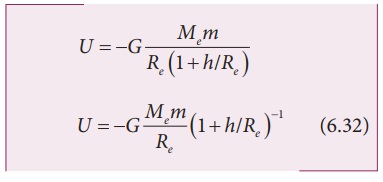
By using Binomial expansion and neglecting the higher order terms, we get

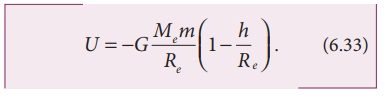
We know that, for a mass m on the Earth’s surface,

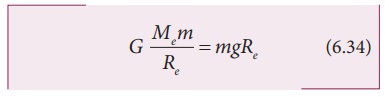
Substituting equation (6.34) in (6.33) we get,

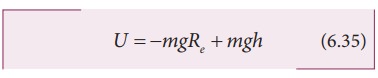
It is clear that the first term in the above expression is independent of the height h. For example, if the object is taken from height h₁ to h_2,then the potential energy at h₁ is

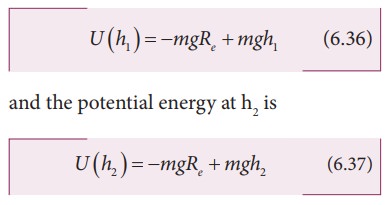
The potential energy difference between h₁ and h₂ is

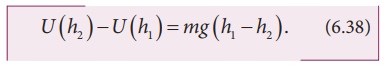
The term mgR_e in equations (6.36) and (6.37) plays no role in the result. Hence in the equation (6.35) the first term can be omitted or taken to zero. Thus it can be stated that The gravitational potential energy stored in the particle of mass m at a height h from the surface of the Earth is U = mgh. On the surface of the Earth, U = 0, since h is zero.

It is to be noted that mgh is the work done on the particle when we take the mass m from the surface of the Earth to a height h. This work done is stored as a gravitational potential energy in the mass m. Even though mgh is gravitational potential energy of the system (Earth and mass m), we can take mgh as the gravitational potential energy of the mass m since Earth is stationary when the mass moves to height h.