Gravitation | Physics - Book Back Numerical Problems | 11th Physics : UNIT 6 : Gravitation
Chapter: 11th Physics : UNIT 6 : Gravitation
Book Back Numerical Problems
Gravitation (Physics)
Numerical Problems
1. An unknown planet orbits the Sun with distance twice the semi major axis distance of the Earth’s orbit. If the Earth’s time period is T1, what is the time period of this unknown planet?
Solution
The earth’s time period = T1
Semi major axis distance of earth = α1
Time period of unknown planet = T2
Semi major axis of unknown planet = 2α1,
Kepler’s III law
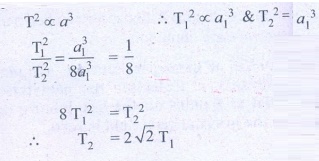
T2 =2√2T1
Ans: T2 = 2 √2T1
2. Assume that you are in another solar system and provided with the set of data given below consisting of the planets’ semi major axes and time periods. Can you infer the relation connecting semi major axis and time period?
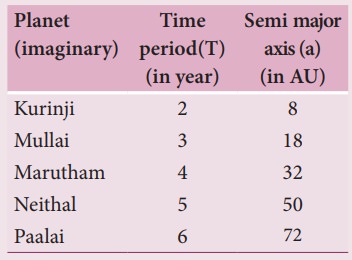
Solution
For planet kurinji
Time period T12 ∝ α13
T1=2;
α1 = 8
α1 = 2.22 => 2.T12
Similarly for other planets
α2 = 2.32 => 2T22
α3 = 2.42 => 2T32
α4 = 2.52 => 2T42
α ∝ 2T2
Ans: a ∝ 2T2
3. If the masses and mutual distance between the two objects are doubled, what is the change in the gravitational force between them?
Answer
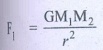
Now the masses and distance between two objects is doubled.
F2 = F1
No change in gravitational force when masses and distance are doubled.
Ans: No change
4. Two bodies of masses m and 4m are placed at a distance r. Calculate the gravitational potential at a point on the line joining them where the gravitional field is zero.
Ans: V = −9Gm/r
5. If the ratio of the orbital distance of two planets d1/d2 =2, what is the ratio of gravitational field experienced by these two planets?
Ans: E2 = 4 E1
6. The Moon Io orbits Jupiter once in 1.769 days. The orbital radius of the Moon Io is 421700 km. Calculate the mass of Jupiter?
Solution
Time period of moon Io = 1.769 days
= 1.769 × 24 × 60 × 60s.
Orbital radius of the moon (r) = 4.217 × 108m.
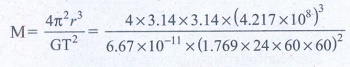
M = 1.898 × 1027kg
Ans: 1.898 ×1027 kg
7. If the angular momentum of a planet is given by 
= 5 t 2iˆ −6tjˆ +3kˆ
. What is the torque experienced by the planet? Will the torque be in the same direction as that of the angular momentum?
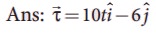
8. Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle
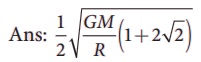
9. Suppose unknowingly you wrote the universal gravitational constant value as G = 6.67x1011 instead of the correct value G = 6.67x10-11 , what is the acceleration due to gravity g' for this incorrect G? According to this new acceleration due to gravity, what will be your weight W'?
Solution:
Mass of the earth M = 6.024 × 1024 kg
Radius of the earth R = 6.4 × 106m
Gravitational constant G' (Incorrect) = 6.67 × 1011
Gravitational constant G (Correct) = 6.67 × 1011
Acceleration due to gravity g' = ?
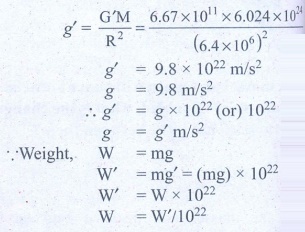
Ans: g' =1022 g, W' = 1022W
10. Calculate the gravitational field at point O due to three masses m1,m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in gravitational field at the point O?
11. What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 × 1024 kg and mass of the Sun is 1.9 × 1030 kg.
Solution:
The distance between sun & Earth R= 150 million km = 150 × 1011m.
The mass of the sun Ms = 1.9 × 1030 kg
The mass of the Earth Me = 5.9 × 1024 kg
The gravitational potential energy U = ?
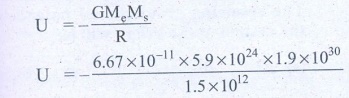
U = -4.985 × 1032 J
P.E U = -49.84 × 1031 J
Ans: V = -49.84 × 1032 Joule
12. Earth revolves around the Sun at 30 km s−1. Calculate the kinetic energy of the Earth. In the previous example you calculated the potential energy of the Earth. What is the total energy of the Earth in that case? Is the total energy positive? Give reasons.
Solution:
The velocity of earth revolves around the sun = v = 30kms (or) 30 × 103 ms-1
K.E of the earth = 1/2 mv2 = ?
Mass of the earth = 5.9 × 1024 kg
K.E = 1/2 × 5.9 × 1024 × 30 × 30 × 1O+3 × 10+3
= 1/2 × 5.9 × 1024 × 900 × 106
= 2655 × 1030 (or) 26.55 × 1032J
T.E = P.E + K.E
= - 49.84 × 1032 + 26.55 × 1032
E = - 23.29 × 1032 J
Ans: K.E = 26.5 × 1032 J
E = −23.29 × 1032 J
( - ) ve implies that Earth is bounded with Sun
13. An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy
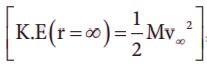with what velocity should the object be thrown from Earth?
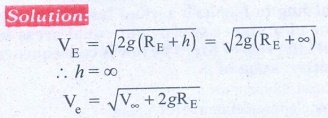
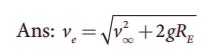
14. Suppose we go 200 km above and below the surface of the Earth, what are the g values at these two points? In which case, is the value of g small?
Ans: gdown = 0.96 g
gup = 0.94 g
15. Calculate the change in g value in your district of Tamil nadu. (Hint: Get the latitude of your district of Tamil nadu from the Google). What is the difference in g values at Chennai and Kanyakumari?
Solution:
Chennai
g'c = g - ω2 R cos2λ
= 9.8 - (3.4 × 10-2)
= 9.7677 ms-2
g'K =9.8 - (3.4x 10-2) × (cos0.1396)2 = 9.748 ms-2
Difference in g value Δg = 0.0331 ms-2
ω2R = (2 × (3.14/86400) )2 × 6400 × 103
λ =13' (or) 0.2268 rad
Ans: gchennai = 9.767 m s-2
gKanyakumari = 9.798 m s-2
Δg = 0.031 m s-2
Related Topics