Chapter: 11th Physics : UNIT 6 : Gravitation
Gravitational potential V(r)
Gravitational
potential V(r)
It
is explained in the previous sections that the gravitational field ![]() depends only on the source mass which
creates the field. It is a vector quantity. We can also define a scalar
quantity called “gravitational potential” which depends only on the source
mass.
depends only on the source mass which
creates the field. It is a vector quantity. We can also define a scalar
quantity called “gravitational potential” which depends only on the source
mass.
The
gravitational potential at a distance r due to a mass is defined as the amount
of work required to bring unit mass from infinity to the distance r and it is
denoted as V(r). In other words, the gravitational potential at distance r is
equivalent to gravitational potential energy per unit mass at the same distance
r. It is a scalar quantity and its unit is J kg-1
![]()
![]() We can determine gravitational potential from gravitational
potential energy. Consider two masses m1 and m2 separated
by a distance r which has gravitational potential energy U( r ) (Figure 6.15). The
gravitational potential due to mass m1 at a point P which is at a
distance r from m1 is obtained by making m2 equal to
unity (m2 = 1kg). Thus the gravitational potential V ( r ) due to mass m1 at a distance r is
We can determine gravitational potential from gravitational
potential energy. Consider two masses m1 and m2 separated
by a distance r which has gravitational potential energy U( r ) (Figure 6.15). The
gravitational potential due to mass m1 at a point P which is at a
distance r from m1 is obtained by making m2 equal to
unity (m2 = 1kg). Thus the gravitational potential V ( r ) due to mass m1 at a distance r is

Gravitational
field and gravitational force are vector quantities whereas the gravitational
potential and gravitational potential energy are scalar quantities. The motion
of particles can be easily analyzed using scalar quantities than vector
quantities. Consider the example of a falling apple:
Figure
6.16 shows an apple which falls on Earth due to Earth’s gravitational force.
This can be explained using the concept of gravitational potential V( r ) as follows.
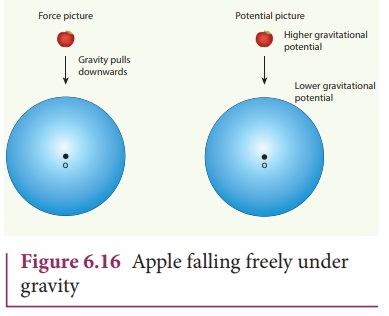
The
gravitational potential V( r ) at a
point of height h from the surface of the Earth is given by,
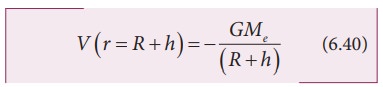
The
gravitational potential Vr on the surface of Earth is given by,
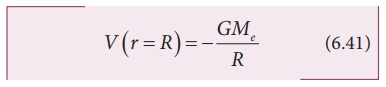
Thus
we see that
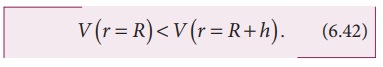
It
is already discussed in the previous section that the gravitational potential
energy near the surface of the Earth at height h is mgh. The
gravitational potential at this point is simply V ( h ) = U ( h) /m = gh. In fact, the gravitational potential
on the surface of the Earth is zero since h
is zero. So the apple falls from a region of a higher gravitational potential
to a region of lower gravitational potential. In general, the mass will move
from a region of higher gravitational potential to a region of lower
gravitational potential.
EXAMPLE 6.5
Water
falls from the top of a hill to the ground. Why?
This
is because the top of the hill is a point of higher gravitational potential
than the surface of the Earth i.e.Vhill
> Vground

The
motion of particles can be analyzed more easily using scalars like U ( r )or V(r) than vector quantities like ![]() or
or ![]() . In modern theories of
physics, the concept of potential plays a vital role.
. In modern theories of
physics, the concept of potential plays a vital role.
EXAMPLE 6.6
Consider
four masses m1, m2, m3, and m4
arranged on the circumference of a circle as shown in figure below
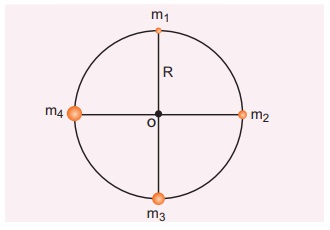
Calculate
a) The gravitational potential energy of the system of 4
masses shown in figure.
b)
The gravitational potential at the point O due to all the 4 masses.
Solution
The
gravitational potential energy U( r )
can be calculated by finding the sum of gravitational potential energy of each
pair of particles.

If
all the masses are equal, then m1 = m2 = m3 =
m4 = M
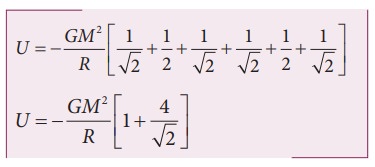
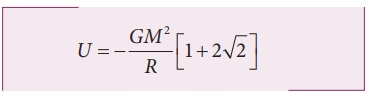
The gravitational potential V(r) at a point O is equal to the sum of the gravitational potentials due to individual mass. Since potential is a scalar, the net potential at point O is the algebraic sum of potentials due to each mass.

Related Topics