Chapter: 11th Physics : UNIT 6 : Gravitation
Superposition principle for Gravitational field
Superposition
principle for
Gravitational field
Consider
ŌĆśnŌĆÖ particles of masses m1
, m2 , .mn, distributed in space at
positions ![]() 1
,
1
, ![]() 2 ,
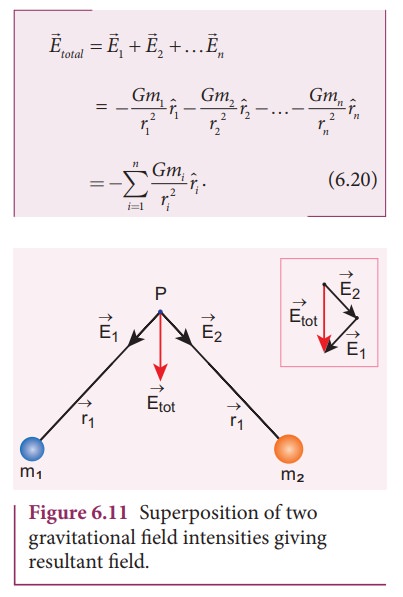
2 , ![]() 3 ŌĆ” etc, with respect to point P. The total gravitational field
at a point P due to all the masses is given by the vector sum of the
gravitational field due to the individual masses (Figure 6.11). This principle
is known as superposition of gravitational fields.
3 ŌĆ” etc, with respect to point P. The total gravitational field
at a point P due to all the masses is given by the vector sum of the
gravitational field due to the individual masses (Figure 6.11). This principle
is known as superposition of gravitational fields.
Instead
of discrete masses, if we have continuous distribution of a total mass M, then
the gravitational field at a point P is calculated using the method of
integration.
EXAMPLE 6.3
a)
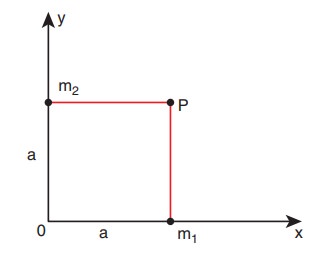
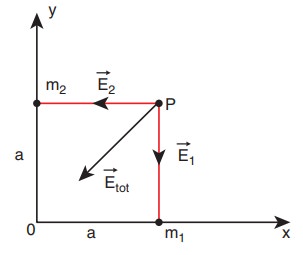
Two particles of masses m1
and m2 are placed along
the x and y axes respectively at a distance ŌĆśaŌĆÖ from the origin. Calculate the
gravitational field at a point P shown in figure below.
Solution
Gravitational
field due to m1 at a point
P is given by,
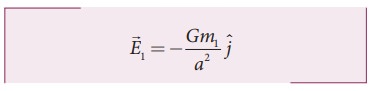
Gravitational
field due to m2 at the
point p is given by,
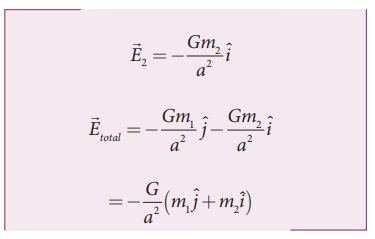
The
direction of the total gravitational field is determined by the relative value
of m1 and m2.
When
m1 = m2 = m
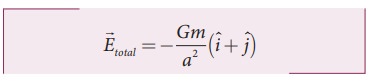
(iˆ
+ jˆ = jˆ + iˆ as vectors obeys commutation law).
![]() total points towards the
origin of the co-ordinate system and the magnitude of
total points towards the
origin of the co-ordinate system and the magnitude of ![]() total
is Gm/a2.
total
is Gm/a2.
EXAMPLE 6.4
Qualitatively
indicate the gravitational field of Sun on Mercury, Earth, and Jupiter shown in
figure.
Since
the gravitational field decreases as distance increases, Jupiter experiences a
weak gravitational field due to the Sun. Since Mercury is the nearest to the
Sun, it experiences the strongest gravitational field.
Related Topics