Satellites, orbital speed and time period

Satellites, orbital speed and time period

We are living in a modern world with sophisticated technological gadgets and are able to communicate to any place on Earth. This advancement was made possible because of our understanding of solar system. Communication mainly depends on the satellites that orbit the Earth (Figure 6.20). Satellites revolve around the Earth just like the planets revolve around the Sun. Kepler’s laws are applicable to man-made satellites also.

For a satellite of mass M to move in a circular orbit, centripetal force must be acting on the satellite. This centripetal force is provided by the Earth’s gravitational force.

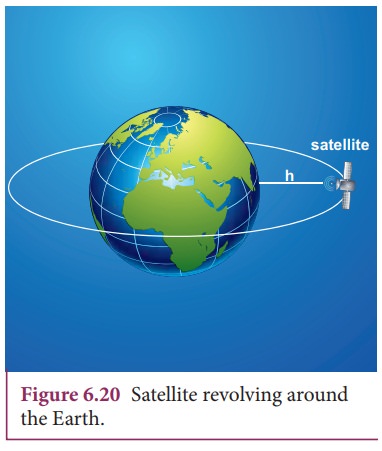
As h increases, the speed of the satellite decreases.

Time period of the satellite:

The distance covered by the satellite during one rotation in its orbit is equal to 2Ï€(RE +h and time taken for it is the time period, T. Then

Squaring both sides of the equation (6.60), we get

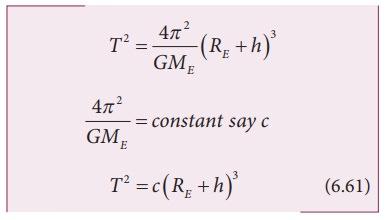
Equation (6.61) implies that a satellite orbiting the Earth has the same relation between time and distance as that of Kepler’s law of planetary motion. For a satellite orbiting near the surface of the Earth, h is negligible compared to the radius of the Earth RE. Then,

By substituting the values of RE = 6.4 Ã— 106m and g = 9.8 m s−2, the orbital time period is obtained as T â‰… 85 minutes.

EXAMPLE 6.9

Moon is the natural satellite of Earth and it takes 27 days to go once around its orbit. Calculate the distance of the Moon from the surface of the Earth assuming the orbit of the Moon as circular.

Solution

We can use Kepler’s third law,

Here h is the distance of the Moon from the surface of the Earth. Here,

By substituting these values, the distance to the Moon from the surface of the Earth is calculated to be 3.77 Ã—105 km.