Gravitation | Physics - Solved Example Problems | 11th Physics : UNIT 6 : Gravitation
Chapter: 11th Physics : UNIT 6 : Gravitation
Solved Example Problems
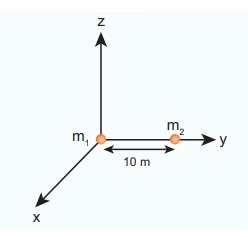
Consider two point masses m1 and m2 which are separated by a distance of 10 meter as shown in the following figure. Calculate the force of attraction between them and draw the directions of forces on each of them. Take m1= 1 kg and m2 = 2 kg
Solution
The force of attraction is given by
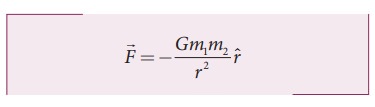
From the figure, r =10 m.
First, we can calculate the magnitude of the force
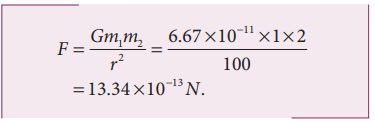
It is to be noted that this force is very small. This is the reason we do not feel the gravitational force of attraction between each other. The small value of G plays a very crucial role in deciding the strength of the force.
The force of attraction (![]() ) experienced by the mass m2 due to m1 is in the negative ŌĆśyŌĆÖ direction ie., r╦å =ŌłÆj╦å . According to NewtonŌĆÖs third law, the mass m2 also exerts equal and opposite force on m1. So the force of attraction (
) experienced by the mass m2 due to m1 is in the negative ŌĆśyŌĆÖ direction ie., r╦å =ŌłÆj╦å . According to NewtonŌĆÖs third law, the mass m2 also exerts equal and opposite force on m1. So the force of attraction (![]() ) experienced by m1 due to m2 is in the direction of positive ŌĆśyŌĆÖ axis ie., r╦å = j╦å .
) experienced by m1 due to m2 is in the direction of positive ŌĆśyŌĆÖ axis ie., r╦å = j╦å .
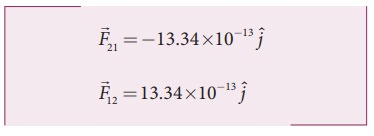
The direction of the force is shown in the figure,
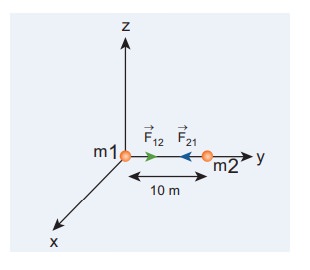
Gravitational force of attraction between m1 and m2
![]() = ŌłÆ
= ŌłÆ![]() which confirms NewtonŌĆÖs third law.
which confirms NewtonŌĆÖs third law.
EXAMPLE 6.2
Moon and an apple are accelerated by the same gravitational force due to Earth. Compare the acceleration of the two.
The gravitational force experienced by the apple due to Earth
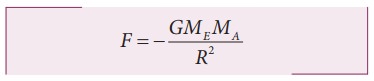
Here MA ŌĆō Mass of the apple, MEŌĆō Mass of the Earth and R ŌĆō Radius of the Earth.
Equating the above equation with NewtonŌĆÖs second law,
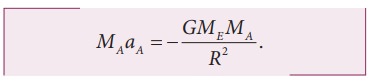
Simplifying the above equation we get,
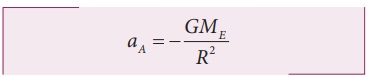
Here aA is the acceleration of apple that is equal to ŌĆśgŌĆÖ.
Similarly the force experienced by Moon due to Earth is given by
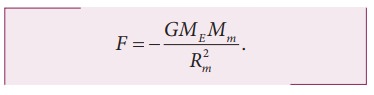
Here Rm- distance of the Moon from the Earth, Mm ŌĆō Mass of the Moon
The acceleration experienced by the Moon is given by
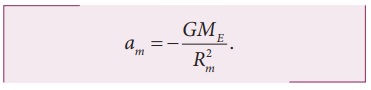
The ratio between the appleŌĆÖs acceleration to MoonŌĆÖs acceleration is given by

From the Hipparchrus measurement, the distance to the Moon is 60 times that of Earth radius. Rm = 60R.

The appleŌĆÖs acceleration is 3600 times the acceleration of the Moon.
The same result was obtained by Newton using his gravitational formula. The appleŌĆÖs acceleration is measured easily and it is 9.8 m sŌłÆ2 . Moon orbits the Earth once in 27.3 days and by using the centripetal acceleration formula, (Refer unit 3).
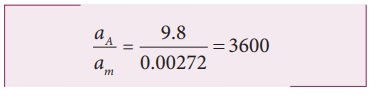
which is exactly what he got through his law of gravitation.
EXAMPLE 6.3
a) Two particles of masses m1 and m2 are placed along the x and y axes respectively at a distance ŌĆśaŌĆÖ from the origin. Calculate the gravitational field at a point P shown in figure below.
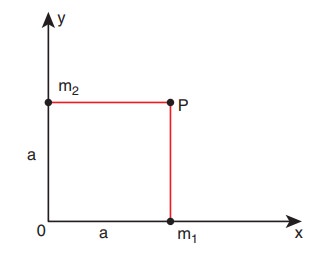
Solution
Gravitational field due to m1 at a point P is given by,

Gravitational field due to m2 at the point p is given by,

The direction of the total gravitational field is determined by the relative value of m1 and m2.
When m1 = m2 = m
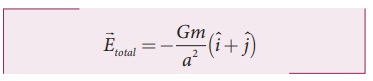
(iˆ + jˆ = jˆ + iˆ as vectors obeys commutation law).
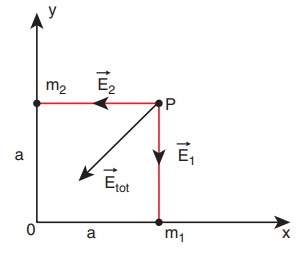
![]() total points towards the origin of the co-ordinate system and the magnitude of
total points towards the origin of the co-ordinate system and the magnitude of ![]() total is Gm/a2.
total is Gm/a2.
EXAMPLE 6.4
Qualitatively indicate the gravitational field of Sun on Mercury, Earth, and Jupiter shown in figure.
Since the gravitational field decreases as distance increases, Jupiter experiences a weak gravitational field due to the Sun. Since Mercury is the nearest to the Sun, it experiences the strongest gravitational field.

EXAMPLE 6.5
Water falls from the top of a hill to the ground. Why?
This is because the top of the hill is a point of higher gravitational potential than the surface of the Earth i.e.Vhill > Vground

The motion of particles can be analyzed more easily using scalars like U ( r )or V(r) than vector quantities like ![]() or
or ![]() . In modern theories of physics, the concept of potential plays a vital role.
. In modern theories of physics, the concept of potential plays a vital role.
EXAMPLE 6.6
Consider four masses m1, m2, m3, and m4 arranged on the circumference of a circle as shown in figure below
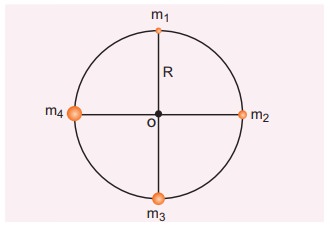
Calculate
a) The gravitational potential energy of the system of 4 masses shown in figure.
b) The gravitational potential at the point O due to all the 4 masses.
Solution
The gravitational potential energy U( r ) can be calculated by finding the sum of gravitational potential energy of each pair of particles.

If all the masses are equal, then m1 = m2 = m3 = m4 = M
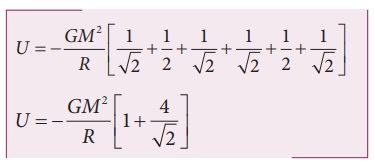
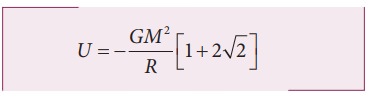
The gravitational potential V(r) at a point O is equal to the sum of the gravitational potentials due to individual mass. Since potential is a scalar, the net potential at point O is the algebraic sum of potentials due to each mass.

EXAMPLE 6.7
1. Calculate the value of g in the following two cases:
a) If a mango of mass ┬Į kg falls from a tree from a height of 15 meters, what is the acceleration due to gravity when it begins to fall?
Solution

b) Consider a satellite orbiting the Earth in a circular orbit of radius 1600 km above the surface of the Earth. What is the acceleration experienced by the satellite due to EarthŌĆÖs gravitational force?
Solution
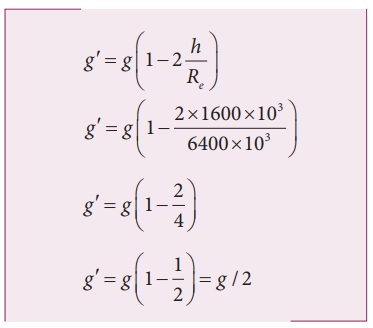
The above two examples show that the acceleration due to gravity is a constant near the surface of the Earth.
EXAMPLE 6.8
Find out the value of gŌĆ▓ in your school laboratory?
Solution
Calculate the latitude of the city or village where the school is located. The information is available in Google search. For example, the latitude of Chennai is approximately 13 degree.
g ŌĆ▓ = g ŌłÆŽē 2 R cos2 ╬╗
Here Žē2R = (2x3.14/86400)2 x (6400x103) = 3.4x10ŌłÆ2 mŌĆåsŌłÆ2.
It is to be noted that the value of ╬╗ should be in radian and not in degree. 13 degree is equivalent to 0.2268 rad.
gŌĆ▓ = 9.8 ŌłÆ ( 3.4 ├Ś 10ŌłÆ2 ) ├Ś ( cos 0.2268)2
g = 9.7677 mŌĆåsŌłÆ2
EXAMPLE 6.9
Moon is the natural satellite of Earth and it takes 27 days to go once around its orbit. Calculate the distance of the Moon from the surface of the Earth assuming the orbit of the Moon as circular.
Solution
We can use KeplerŌĆÖs third law,

Here h is the distance of the Moon from the surface of the Earth. Here,

By substituting these values, the distance to the Moon from the surface of the Earth is calculated to be 3.77 ├Ś105 km.
EXAMPLE 6.10
Calculate the energy of the (i) Moon orbiting the Earth and (ii) Earth orbiting the Sun.
Solution
Assuming the orbit of the Moon to be circular, the energy of Moon is given by,
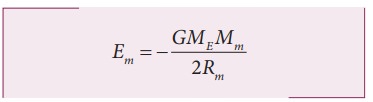
where ME is the mass of Earth 6.02 ├Ś1024 kg; Mm is the mass of Moon 7.35 ├Ś1022 kg; and R is the distance between the Moon and the center of the Earth 3.84 ├Ś105 km
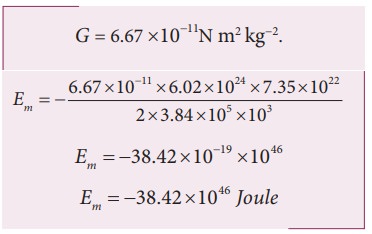
The negative energy implies that the Moon is bound to the Earth.
Same method can be used to prove that the energy of the Earth is also negative.
Gravitation (Physics)
Numerical Problems
1. An unknown planet orbits the Sun with distance twice the semi major axis distance of the EarthŌĆÖs orbit. If the EarthŌĆÖs time period is T1, what is the time period of this unknown planet?
Solution
The earthŌĆÖs time period = T1
Semi major axis distance of earth = ╬▒1
Time period of unknown planet = T2
Semi major axis of unknown planet = 2╬▒1,
KeplerŌĆÖs III law
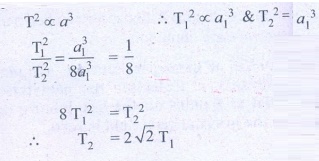
T2 =2ŌłÜ2T1
Ans: T2 = 2 ŌłÜ2T1
2. Assume that you are in another solar system and provided with the set of data given below consisting of the planetsŌĆÖ semi major axes and time periods. Can you infer the relation connecting semi major axis and time period?
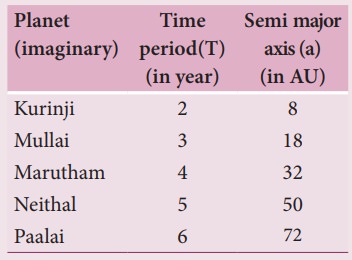
Solution
For planet kurinji
Time period T12 ŌłØ ╬▒13
T1=2;
╬▒1 = 8
╬▒1 = 2.22 => 2.T12
Similarly for other planets
╬▒2 = 2.32 => 2T22
╬▒3 = 2.42 => 2T32
╬▒4 = 2.52 => 2T42
╬▒ ŌłØ 2T2
Ans: a ŌłØ 2T2
3. If the masses and mutual distance between the two objects are doubled, what is the change in the gravitational force between them?
Answer
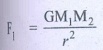
Now the masses and distance between two objects is doubled.

F2 = F1
No change in gravitational force when masses and distance are doubled.
Ans: No change
4. Two bodies of masses m and 4m are placed at a distance r. Calculate the gravitational potential at a point on the line joining them where the gravitional field is zero.

Ans: V = ŌłÆ9Gm/r
5. If the ratio of the orbital distance of two planets d1/d2 =2, what is the ratio of gravitational field experienced by these two planets?

Ans: E2 = 4 E1
6. The Moon Io orbits Jupiter once in 1.769 days. The orbital radius of the Moon Io is 421700 km. Calculate the mass of Jupiter?
Solution
Time period of moon Io = 1.769 days
= 1.769 ├Ś 24 ├Ś 60 ├Ś 60s.
Orbital radius of the moon (r) = 4.217 ├Ś 108m.
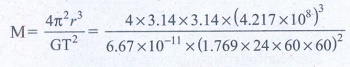
M = 1.898 ├Ś 1027kg
Ans: 1.898 ├Ś1027 kg
7. If the angular momentum of a planet is given by ![]() = 5 t 2i╦å ŌłÆ6tj╦å +3k╦å
= 5 t 2i╦å ŌłÆ6tj╦å +3k╦å![]() . What is the torque experienced by the planet? Will the torque be in the same direction as that of the angular momentum?
. What is the torque experienced by the planet? Will the torque be in the same direction as that of the angular momentum?

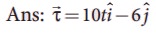
8. Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. Calculate the speed of each particle

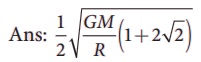
9. Suppose unknowingly you wrote the universal gravitational constant value as G = 6.67x1011 instead of the correct value G = 6.67x10-11 , what is the acceleration due to gravity g' for this incorrect G? According to this new acceleration due to gravity, what will be your weight W'?
Solution:
Mass of the earth M = 6.024 ├Ś 1024 kg
Radius of the earth R = 6.4 ├Ś 106m
Gravitational constant G' (Incorrect) = 6.67 ├Ś 1011
Gravitational constant G (Correct) = 6.67 ├Ś 1011
Acceleration due to gravity g' = ?
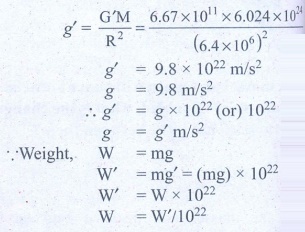
Ans: g' =1022 g, W' = 1022W
10. Calculate the gravitational field at point O due to three masses m1,m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in gravitational field at the point O?


11. What is the gravitational potential energy of the Earth and Sun? The Earth to Sun distance is around 150 million km. The mass of the Earth is 5.9 ├Ś 1024 kg and mass of the Sun is 1.9 ├Ś 1030 kg.
Solution:
The distance between sun & Earth R= 150 million km = 150 ├Ś 1011m.
The mass of the sun Ms = 1.9 ├Ś 1030 kg
The mass of the Earth Me = 5.9 ├Ś 1024 kg
The gravitational potential energy U = ?
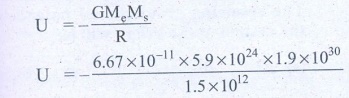
U = -4.985 ├Ś 1032 J
P.E U = -49.84 ├Ś 1031 J
Ans: V = -49.84 ├Ś 1032 Joule
12. Earth revolves around the Sun at 30 kmŌĆåsŌłÆ1. Calculate the kinetic energy of the Earth. In the previous example you calculated the potential energy of the Earth. What is the total energy of the Earth in that case? Is the total energy positive? Give reasons.
Solution:
The velocity of earth revolves around the sun = v = 30kms (or) 30 ├Ś 103 ms-1
K.E of the earth = 1/2 mv2 = ?
Mass of the earth = 5.9 ├Ś 1024 kg
K.E = 1/2 ├Ś 5.9 ├Ś 1024 ├Ś 30 ├Ś 30 ├Ś 1O+3 ├Ś 10+3
= 1/2 ├Ś 5.9 ├Ś 1024 ├Ś 900 ├Ś 106
= 2655 ├Ś 1030 (or) 26.55 ├Ś 1032J
T.E = P.E + K.E
= - 49.84 ├Ś 1032 + 26.55 ├Ś 1032
E = - 23.29 ├Ś 1032 J
Ans: K.E = 26.5 ├Ś 1032 J
E = ŌłÆ23.29 ├Ś 1032 J
( - ) ve implies that Earth is bounded with Sun
13. An object is thrown from Earth in such a way that it reaches a point at infinity with non-zero kinetic energy
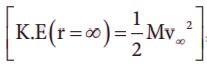 with what velocity should the object be thrown from Earth?
with what velocity should the object be thrown from Earth?
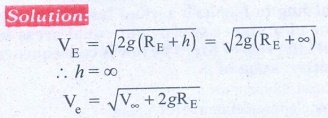
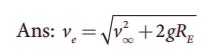
14. Suppose we go 200 km above and below the surface of the Earth, what are the g values at these two points? In which case, is the value of g small?

Ans: gdown = 0.96 g
gup = 0.94 g
15. Calculate the change in g value in your district of TamilŌĆånadu. (Hint: Get the latitude of your district of Tamil nadu from the Google). What is the difference in g values at Chennai and Kanyakumari?
Solution:
Chennai
g'c = g - Žē2 R cos2╬╗
= 9.8 - (3.4 ├Ś 10-2)
= 9.7677 ms-2
g'K =9.8 - (3.4x 10-2) ├Ś (cos0.1396)2 = 9.748 ms-2
Difference in g value Δg = 0.0331 ms-2
Žē2R = (2 ├Ś (3.14/86400) )2 ├Ś 6400 ├Ś 103
╬╗ =13' (or) 0.2268 rad
Ans: gchennai = 9.767 m s-2
gKanyakumari = 9.798 m s-2
Δg = 0.031 m s-2
Related Topics