Kepler’s Laws of Planetary Motion

Kepler’s Laws of Planetary Motion

Kepler’s laws are stated as follows:

1. Law of orbits:

Each planet moves around the Sun in an elliptical orbit with the Sun at one of the foci.

The closest point of approach of the planet to the Sun ‘P’ is called perihelion and the farthest point ‘A’ is called aphelion (Figure 6.1). The semi-major axis is ‘a’ and semi-minor axis is ‘b’. In fact, both Copernicus and Ptolemy considered planetary orbits to be circular, but Kepler discovered that the actual orbits of the planets are elliptical. 

2. Law of area:

The radial vector (line joining the Sun to a planet) sweeps equal areas in equal intervals of time.

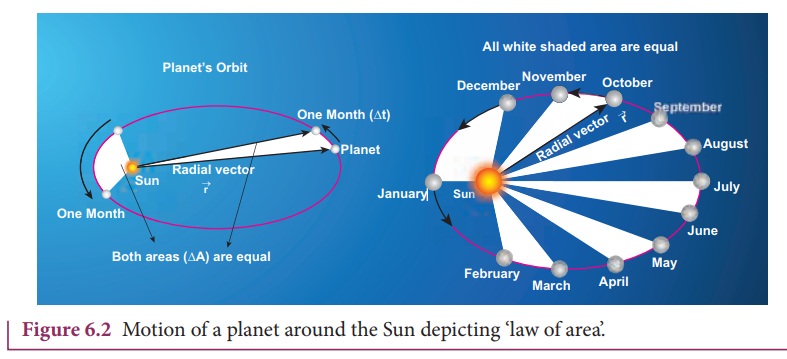
In Figure 6.2, the white shaded portion is the area âˆ†A swept in a small interval of time âˆ†t, by a planet around the Sun. Since the Sun is not at the center of the ellipse, the planets travel faster when they are nearer to the Sun and slower when they are farther from it, to cover equal area in equal intervals of time. Kepler discovered the law of area by carefully noting the variation in the speed of planets.

3. Law of period:

The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse. It can be written as:

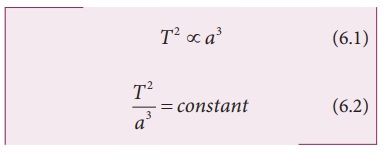
where, T is the time period of revolution for a planet and a is the semi-major axis. Physically this law implies that as the distance of the planet from the Sun increases, the time period also increases but not at the same rate.

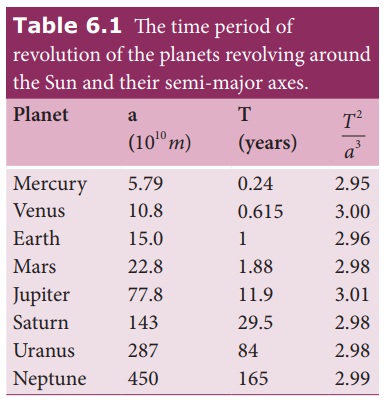
In Table 6.1, the time period of revolution of planets around the Sun along with their semi-major axes are given. From column four, we can realize that T2/a3,is nearly a constant endorsing Kepler’s third law.