Elementary Ideas of Astronomy

ELEMENTARY IDEAS OF ASTRONOMY

Astronomy is one of the oldest sciences in the history of mankind. In the olden days, astronomy was an inseparable part of physical science. It contributed a lot to the development of physics in the 16th century. In fact Kepler’s laws and Newton’s theory of gravitation were formulated and verified using astronomical observations and data accumulated over the centuries by famous astronomers like Hippachrus, Aristachrus, Ptolemy, Copernicus and Tycho Brahe. Without Tycho Brahe’s astronomical observations, Kepler’s laws would not have emerged. Without Kepler’s laws, Newton’s theory of gravitation would not have been formulated.

It was mentioned in the beginning of this chapter that Ptolemy’s geocentric model was replaced by Copernicus’ heliocentric model. It is important to analyze and explain the shortcoming of the geocentric model over heliocentric model.

Heliocentric system over geocentric system

When the motion of the planets are observed in the night sky by naked eyes over a period of a few months, it can be seen that the planets move eastwards and reverse their motion for a while and return to eastward motion again. This is called “retrograde motion” of planets.

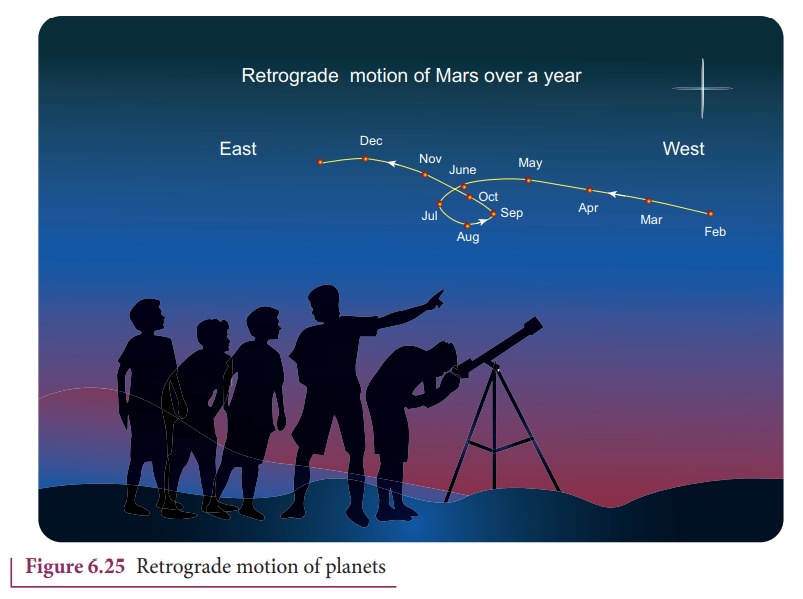
Figure 6.25 shows the retrograde motion of the planet Mars. Careful observation for a period of a year clearly shows that Mars initially moves eastwards (February to June), then reverses its path and moves backwards (July, August, September). It changes its direction of motion once again and continues its forward motion (October onwards) . In olden days, astronomers recorded the retrograde motion of all  visible planets and tried to explain the motion. According to Aristotle, the other planets and the Sun move around the Earth in the circular orbits.

If it was really a circular orbit it was not known how the planet could reverse its motion for a brief interval. To explain this retrograde motion, Ptolemy introduced the concept of “epicycle” in his geocentric model. According to this theory, while the planet orbited the Earth, it also underwent another circular motion termed as “epicycle”. A combination of epicycle and circular motion around the Earth gave rise to retrograde motion of the planets with respect to Earth (Figure 6.26). Essentially Ptolemy retained the Earth centric idea of Aristotle and added the epicycle motion to it.

But Ptolemy’s model became more and more complex as every planet was found to undergo retrograde motion. In the 15th century, the Polish astronomer Copernicus proposed the heliocentric model to explain this problem in a simpler manner. According to this model, the Sun is at the center of the solar system and all planets orbited the Sun. The retrograde motion of planets with respect to Earth is because of the relative motion of the planet with respect to Earth. The retrograde motion from the heliocentric point of view is shown in Figure 6.27.

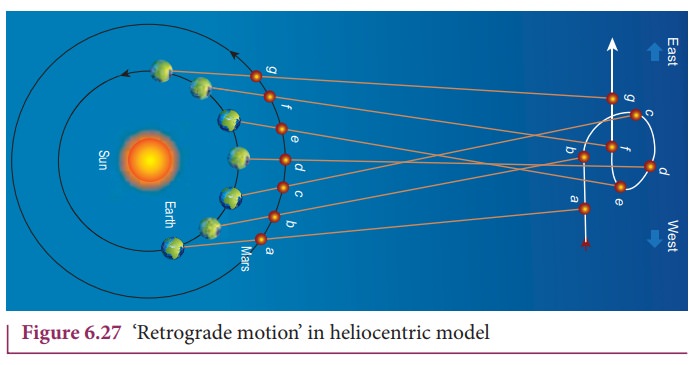
Figure 6.27 shows that the Earth orbits around the Sun faster than Mars. Because of the relative motion between Mars and Earth, Mars appears to move backwards from July to October. In the same way the retrograde motion of all other planets was explained successfully by the Copernicus model. It was because of its simplicity, the heliocentric model slowly replaced the geocentric model. Historically, if any natural phenomenon has one or more explanations, the simplest one is usually accepted. Though this was not the only reason to disqualify the geocentric model, a detailed discussion on correctness of the Copernicus model over to Ptolemy’s model can be found in astronomy books.

Kepler’s Third Law and The Astronomical Distance

When Kepler derived his three laws, he strongly relied on Tycho Brahe’s astronomical observation. In his third law, he formulated the relation between the distance of a planet from the Sun to the time period of revolution of the planet. Astronomers cleverly used geometry and trigonometry to calculate the distance of a planet from the Sun in terms of the distance between Earth and Sun. Here we can see how the distance of Mercury and Venus from the Sun were measured. 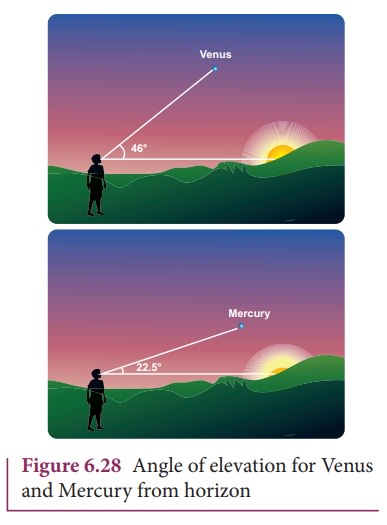The Venus and Mercury, being inner planets with respect to Earth, the maximum angular distance they can subtend at a point on Earth with respect to the Sun is 46 degree for Venus and 22.5 degree for Mercury. It is shown in the Figure 6.28

Figure 6.29 shows that when Venus is at maximum elongation (i.e., 46 degree) with respect to Earth, Venus makes 90 degree to Sun. This allows us to find the distance between Venus and Sun. The distance between Earth and Sun is taken as one Astronomical unit (1 AU).

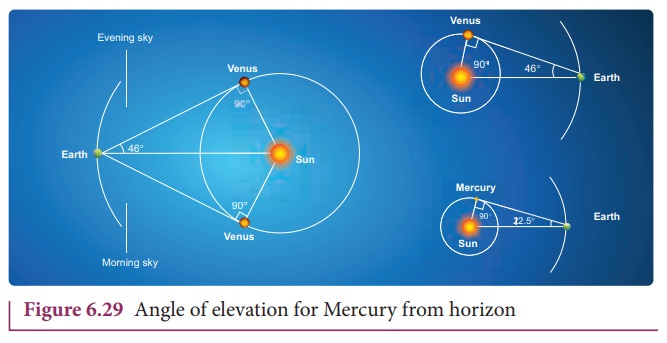
The trigonometric relation satisfied by this right angled triangle is shown in Figure 6.29.

Here sin 46̊ = 0.77. Hence Venus is at a distance of 0.77 AU from Sun. Similarly, the distance between Mercury (θ is 22.5 degree) and Sun is calculated as 0.38 AU. To find the distance of exterior planets like Mars and Jupiter, a slightly different method is used. The distances of planets from the Sun is given in the table below.

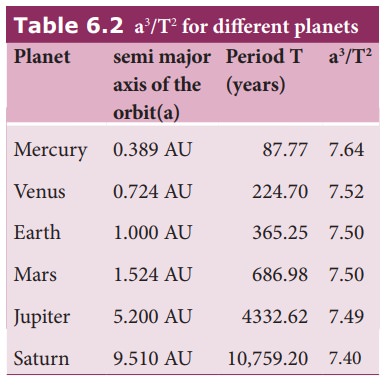
It is to be noted that to verify the Kepler’s law we need only high school level geometry and trigonometry.

Measurement of radius of the Earth

Around 225 B.C a Greek librarian “Eratosthenes” who lived at Alexandria measured the radius of the Earth with a small error when compared with results using modern measurements. The technique he used involves lower school geometry and brilliant insight. 

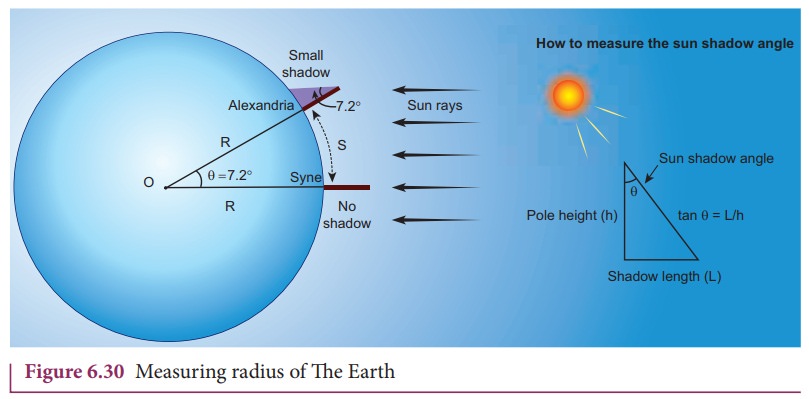
He observed that during noon time of summer solstice the Sun’s rays cast no shadow in the city Syne which was located 500 miles away from Alexandria. At the same day and same time he found that in Alexandria the Sun’s rays made 7.2 degree with local vertical as shown in the Figure 6.30. He realized that this difference of 7.2 degree was due to the curvature of the Earth.

The angle 7.2 degree is equivalent to 1/8 radian. So θ=1/8 rad;

If S is the length of the arc between the cities of Syne and Alexandria, and if R is radius of Earth, then

 1 mile is equal to 1.609 km. So, he measured the radius of the Earth to be equal to R = 6436 km, which is amazingly close to the correct value of 6378 km.

The distance of the Moon from Earth was measured by a famous Greek astronomer Hipparchus in the 3rd century BC.

Interesting Astronomical Facts

1. Lunar eclipse and measurement of shadow of Earth

On January 31, 2018 there was a total lunar eclipse which was observed from various places including Tamil Nadu. It is possible to measure the radius of shadow of the Earth at the point where the Moon crosses. Figure 6.31 illustrates this.

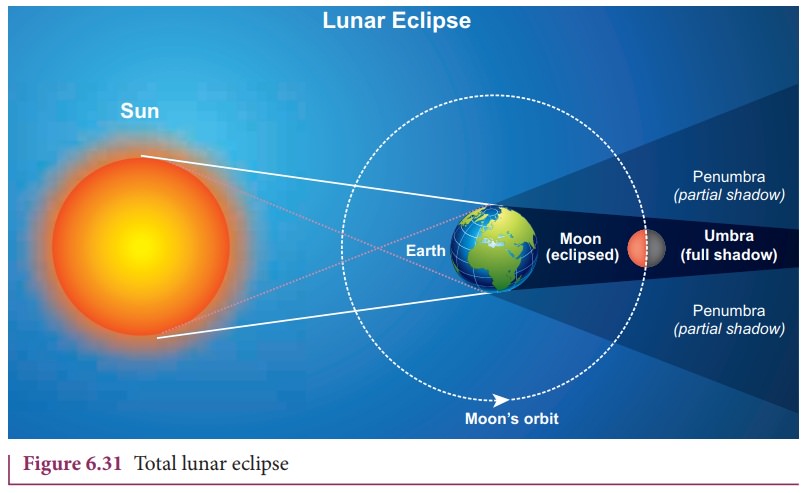
When the Moon is inside the umbra shadow, it appears red in color. As soon as the Moon exits from the umbra shadow, it appears in crescent shape. Figure 6.32 is the photograph taken by digital camera during Moon’s exit from the umbra shadow.

By finding the apparent radii of the Earth’s umbra shadow and the Moon, the ratio of the these radii can be calculated. This is shown in Figures 6.33 and 6.34.

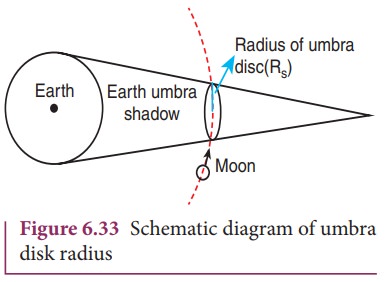
The apparent radius of Earth’s umbra shadow = R_s = 13.2 cm

The apparent radius of the Moon = R_m= 5.15 cm

The ratio R_s/R_m ≈ 2.56

The radius of the Earth’s umbra shadow is R_s = 2.56 x R_m

The radius of Moon R_m = 1737 km

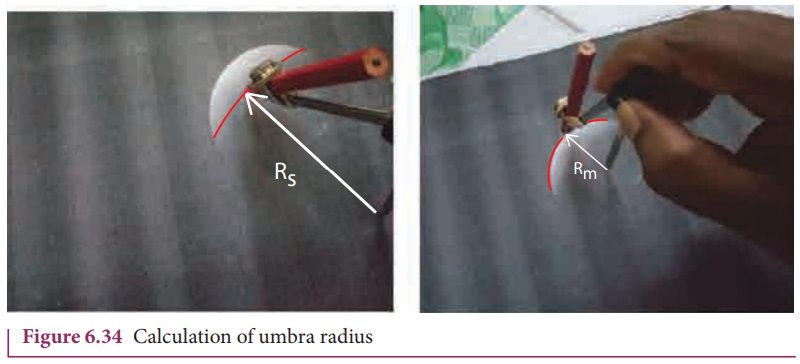
The radius of the Earth’s umbra shadow is Rs = 2.56x1737km ~≡4446 km.

The correct radius is 4610 km.

The percentage of error in the calculation = [ (4610 – 4446) / 4610 ] x 100 = 3.5% . 

The error will reduce if the pictures taken using a high quality telescope are used. It is to be noted that this calculation is done using very simple mathematics.

 Early astronomers proved that Earth is spherical in shape by looking at the shape of the shadow cast by Earth on the Moon during lunar eclipse.

2. Why there are no lunar eclipse and solar eclipse every month? 

If the orbits of the Moon and Earth lie on the same plane, during full Moon of every month, we can observe lunar eclipse.

If this is so during new Moon we can observe solar eclipse. But Moon’s orbit is tilted 5° with respect to Earth’s orbit. Due to this 5° tilt, only during certain periods of the year, the Sun, Earth and Moon align in straight line leading to either lunar eclipse or solar eclipse depending on the alignment. This is shown in Figure 6.35

3.  Why do we have seasons on Earth?

The  common  misconception  is  that ‘Earth revolves around the Sun, so when the Earth is very far away, it is winter and when the Earth is nearer, it is summer’.

Actually, the seasons in the Earth arise due to the rotation of Earth around the Sun with 23.5° tilt. This is shown in Figure 6.36

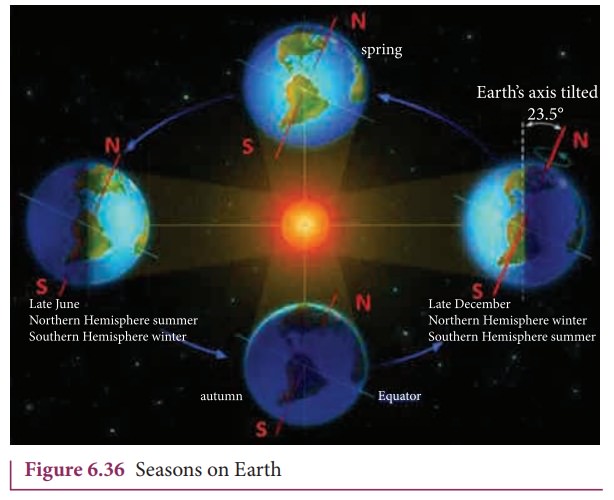
Due  to  this  23.5°  tilt,  when  the northern part of Earth is farther to the Sun, the southern part is nearer to the Sun. So when it is summer in the northern  hemisphere,  the  southern hemisphere experience winter.

4.  Star’s apparent motion and spinning of the Earth

The Earth’s spinning motion can be proved by observing star’s position over a night. Due to Earth’s spinning motion, the stars in sky appear to move in circular motion about the pole star as shown in Figure 6.37

Recent developments of astronomy and gravitation

Till the 19th century astronomy mainly depended upon either observation with the naked eye or telescopic observation. After the discovery of the electromagnetic spectrum at the end of the 19th century, our understanding of the universe increased enormously. Because of this development in the late 19th century it was found that Newton’s law of gravitation could not explain certain phenomena and showed some discrepancies. Albert Einstein formulated his ‘General theory of relativity’ which was one of the most successful theories of 20th century in the field of gravitation.

In the twentieth century both astronomy and gravitation merged together and have grown in manifold. The birth and death of stars were more clearly understood. Many Indian physicists made very important contributions to the field of astrophysics and gravitation.

Subramanian Chandrasekar formulated the theory of black holes and explained the life of stars. These studies brought him the Nobel prize in the year 1983. Another very notable Indian astrophysicist Meghnad Saha discovered the ionization formula which was useful in classifying stars. This formula is now known as “Saha ionization formula”. In the field of gravitation Amal Kumar Raychaudhuri solved an equation now known as “Raychaudhuri equation” which was a very important contribution. Another notable Indian Astrophysicist Jayant V Narlikar made pioneering contribution in the field of astrophysics and has written interesting books on astronomy and astrophysics. IUCAA (Inter University Center for Astronomy and Astrophysics) is one of the important Indian research institutes where active research in astrophysics and gravitation are conducted. The institute was founded by Prof. J.V. Narlikar. Students are encouraged to read more about the recent developments in these fields.