Stoke's law (for highly viscous liquids)

Stoke's law (for highly viscous liquids)

When a body falls through a highly viscous liquid, it drags the layer of the liquid immediately in contact with it. This results in a relative motion between the different layers of the liquid. As a result of this, the falling body experiences a viscous force F. Stoke performed many experiments on the motion of small spherical bodies in different fluids and concluded that the viscous force F acting on the spherical body depends on

(i)    Coefficient of viscosity η of the liquid

(ii) Radius a of the sphere and

(iii)                       Velocity v of the spherical body. Dimensionally it can be proved that

F = k ηav

Experimentally Stoke found that

k = 6π

F = 6π ηav

This is Stoke's law.

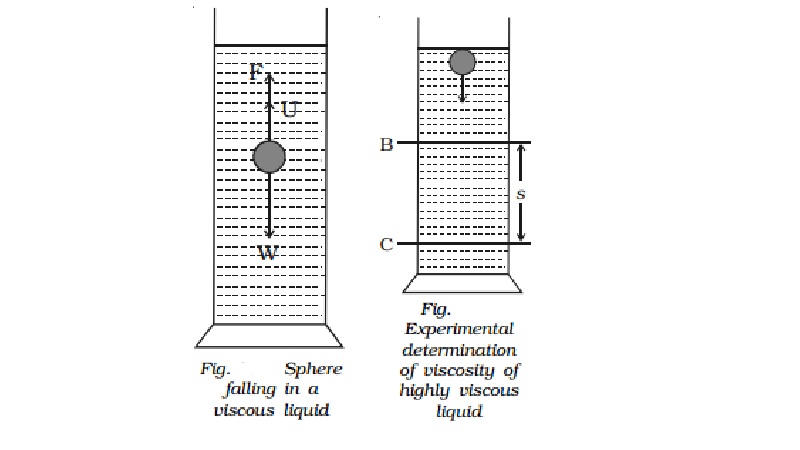
Expression for terminal velocity

Consider a metallic sphere of radius 'a' and density ρ to fall under gravity in a liquid of density σ. The viscous force F acting on the metallic sphere increases as its velocity increases. A stage is reached when the weight W of the sphere becomes equal to the sum of the upward viscous force F and the upward thrust U due to buoyancy (Fig.). Now, there isno net force acting on the sphere and it moves down with a constant velocity v called terminal velocity.

W - F - U = O                ...(1)

Terminal velocity of a body is defined as the constant velocity acquired by a body while falling through a viscous liquid.

From (1), W = F + U            ….. ...(2)

According to Stoke's law, the viscous force F is given by F = 6πηav.

The buoyant force U = Weight of liquid displaced by the sphere

= 4/3  πa³σ g

The weight of the sphere W = 4/3 πa³ρg

Substituting in equation (2)

4/3 πa ρg = 6π ηav +4/3 πa³ σ g

∴ v = 2 a²(ρ- σ)g  / 9η

Experimental determination of viscosity of highly viscous liquids

The coefficient of highly viscous liquid like castoroil can be determined by Stoke's method. The experimental liquid is taken in a tall, wide jar. Two marking B and C are marked as shown in Fig.. A steel ball is gently dropped in the jar.

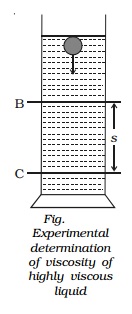
The marking B is made well below the free surface of the liquid so that by the time ball reaches B, it would have acquired terminal velocity v.

When the ball crosses B, a stopwatch is switched on and the time taken t to reach C is noted. If the distance BC is s, then terminal velocity v =s / t .

The expression for terminal velocity is

v = 2 a²(ρ- σ)g  / 9η

η = 2/9 . 2 a²(ρ- σ)g . t/s

Knowing a, ρ and σ, the value of η of the liquid is determined.

Application of Stoke's law

Falling of rain drops: When the water drops are small in size, their terminal velocities are small. Therefore they remain suspended in air in the form of clouds. But as the drops combine and grow in size, their terminal velocities increases because v α a². Hence they start falling as rain.