Sommerfeld atom model and its Drawbacks

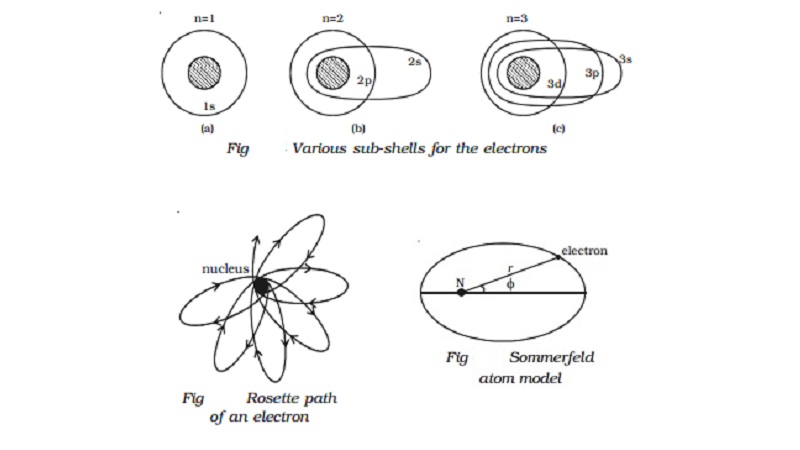
Sommerfeld atom model

In order to explain the observed fine structure of spectral lines, Sommerfeld introduced two main modifications in Bohr's theory.

(i)    According to Sommerfeld, the path of an electron around the nucleus, in general, is an ellipse with the nucleus at one of its foci.

(ii) The velocity of the electron moving in an elliptical orbit varies at different parts of the orbit. This causes the relativistic variation in the mass of the moving electron.

Now, when elliptical orbits are permitted, one has to deal with two variable quantities.

(i)    The varying distance of the electron from the nucleus (r).

(ii) The varying angular position of the electron with respect to the nucleus i.e the azimuthal angle φ (Fig).

To deal with these two variables, two quantum numbers are introduced       

(i) The principal quantum number n of  Bohr's  theory,  which  determines  the energy  of  the  electrons,  and 

(ii) a new quantum number called orbital (or azimuthal) quantum number (l) which has been   introduced to characterize the angular momentum in an orbit i.e., it determines the orbital angular momentum of the electron. Its values vary from zero to (n-1) in steps of unity.

This orbital quantum number (l) is useful in finding the possible elliptical orbits. The possible elliptical orbits are such that

b/a = l+1/n

where a and b are semi-major and semi-minor axes respectively of the ellipse.

According to Sommerfeld's model, for any principal quantum number n, there are n possible orbits of varying eccentricities called sub-orbits or sub-shells. Out of n subshells, one is circular and the remaining (i.e., n-1) are elliptical in shape.

These possible sub-orbits possess slightly different energies because of the relativistic variation of the electron mass.

Consider the first energy level (n=1). When n = 1, l = 0 i.e., in this energy level, there is only one orbit or sub-shell for the electron. Also, when a = b, the two axes of the ellipse are equal. As a result of this, the orbit corresponding to n=1 is circular. This subshell is designated as s sub-shell. Since, this sub-shell belongs to n=1, it is designated as 1s (Fig a).

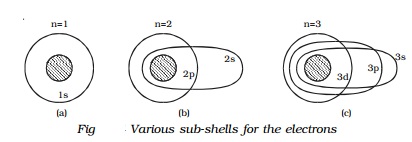
Similarly, for the second energy level n=2, there are two permissible sub-shells for the electrons. For n=2, l can take two values, 0 and 1.

When n = 2, l = 0.

b/a= 0+1/2 =1/2

or

b=a/2

This subshell corresponding to l = 0 is elliptical in shape and is designated as 2s.

when n = 2, l = 1.

b/a= 1+1/2 =2/2 =1

or

b=a

This sub-shell corresponding to l = 1 is circular in shape and is designated as 2p (Fig b).

For n = 3, l has three values 0, 1 and 2, i.e. there are three permissible sub-shells for the electrons.

when      n = 3, l = 0.

b/a= (0+1)/3 =1/3 =1  or b=a/3

 when n = 3, l = 1.

b/a= (1+1)/3 =2/3 =1  or b=2a/3

and when n = 3, l = 2.

b/a= (2+1)/3 =3/3 =1  or b=a

The sub-shells corresponding to l = 0, 1 and 2 are designated as 3s, 3p and 3d respectively. The circular shell is designated as 3d and the other two are elliptical in shape (Fig c).

It is common practice to assign letters to l-values as given below:

Orbital quantum number l         :         0        1        2        3        4

electron state :         s        p       d        f        g

Hence, electrons in the l = 0, 1, 2, 3 … states are said to be in the s, p, d, f … states.

Fine structure of spectral line

Based on Sommerfeld atom model, the total energy of an electron in the elliptical orbit can be shown as,

En = (-me⁴Z² )  /  (8ε₀²h²n²)

This expression is the same as that obtained by Bohr. Thus the introduction of elliptical orbits gives no new energy levels and hence no new transition. In this way, the attempt of Sommerfeld to explain the fine structure of spectral lines failed. But soon, on the basis of variation of mass of electron with velocity, Sommerfeld could find the solution for the problem of the fine structure of the spectral lines.

According to Sommerfeld, the velocity of the electron is maximum when the electron is nearest to the nucleus and minimum when it is farthest from the nucleus, since the orbit of the electron is elliptical. This implies that the effective mass of the electron will be different at different parts of its orbit. 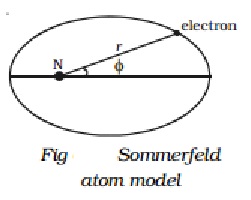Taking into account the relativistic variation of         the     mass of the electron, Sommerfeld modified his theory and showed that the path of electron is not a simple ellipse but a precessing ellipse called a rosette (Fig).

Based on this idea, Sommerfeld successfully explained the fine structure of spectral lines of hydrogen atom.

Drawbacks

(i)                Though Sommerfeld's modification gave a theoretical background of the fine structure of spectral lines of hydrogen, it could not predict the correct number of observed fine structure of these lines.

(ii)             It could not explain the distribution and arrangement of electrons in atoms.

(iii)           Sommerfeld's model was unable to explain the spectra of alkali metals such as sodium, potassium etc.

(iv)           It could not explain Zeeman and Stark effect.

(v)             This model does not give any explanation for the intensities of the spectral lines.