Bragg's law for X-ray diffraction

Bragg's law for X-ray diffraction

W.L. Bragg and W.H. Bragg studied the diffraction of X-rays in detail and used a crystal of rock salt to diffract X-rays and succeeded in measuring the wavelength of X-rays.

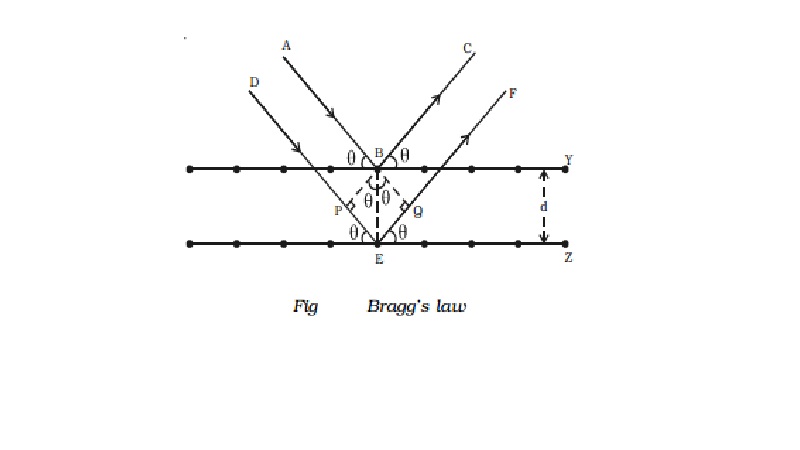
Consider homo-geneous X-rays of wave length λ incident on a crystal at a glancing angle θ. The incident rays AB and DE after reflection from the lattice planes Y and Z travel along BC and EF respectively as shown in Fig .

Let the crystal lattice spacing between the planes be d. BP and BQ are perpendiculars drawn from B on DE and EF respectively. Therefore, the path difference between the two waves ABC and DEF is equal to PE + EQ.

In the ∆PBE, sin θ = PE/BE (or) PE = BE sin θ = d sin θ

In the ∆QBE, sin θ = EQ/BE (or) EQ = BE sin θ = d sin θ

Path difference = PE + EQ = d sin θ + d sin θ = 2d sin θ

If this path difference 2d sin θ is equal to integral multiple of wavelength of X-ray i.e. nλ, then constructive interference will occur between the reflected beams and they will reinforce with each other. Therefore the intensity of the reflected beam is maximum.

2d sin θ = nλ where, n = 1, 2, 3

etc. This is known as Bragg's law.