Photoelectric effect - Dual Nature of Radiation

Dual Nature of Radiation and Matter and Relativity

The true nature of light is difficult to assess. Experiments showed that light exhibited wavelike properties of diffraction and interference. On the other hand, photoelectric effect indicates that light has the aspects of a particle photon, with both energy and momentum. Thus light exhibits a wave-particle duality.

The wave-particle duality was extended to particles as matter waves by Louis de Broglie. His theoretical study on the nature of particles and waves led to the invention of a new mechanics of particles called quantum mechanics.

Photoelectric effect

Photoelectric emission is the phenomena by which a good number of substances, chiefly metals, emit electrons under the influence of radiation such as γ rays, X-rays, ultraviolet and even visible light. This effect was discovered by Heinrich Hertz in 1887 while working with resonance electrical circuits. A year later, Hallwachs, Elster and Geitel investigated the phenomenon with a simple experimental arrangement.

Hallwachs Experiment

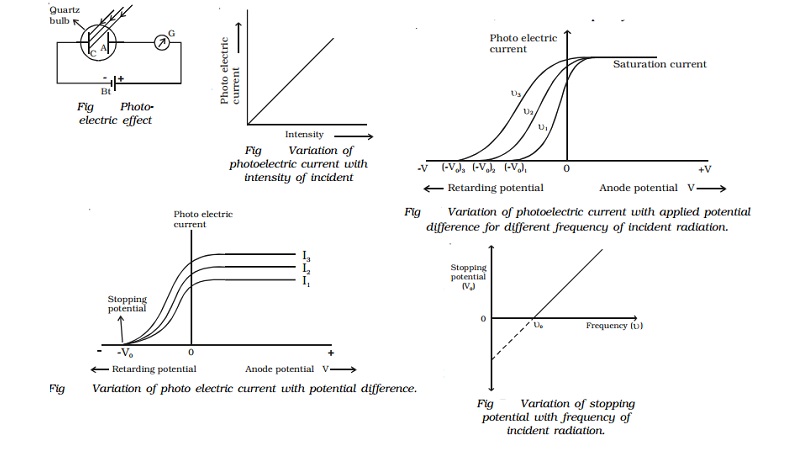
Hallwachs experimental set-up to study the photo electric effect is shown in Fig  It consists of an evacuated quartz bulb with two zinc plates cathode C and anode A. The plates are connected to a battery and a sensitive galvanometer. In the absence  of  any  radiation  incident  on  the plates, there is no flow of current and hence there is no deflection in the galvanometer.

But, when an electro magnetic radiation like ultraviolet radiation is allowed to fall on the plate C which is connected to the negative terminal of the battery, a current begins to flow, indicated by the deflection in the galvanometer (G). But, when ultraviolet radiation is made to fall on A, there is no deflection in the galvanometer. These observations reveal that the particles emitted by the plate C due to the photoelectric effect are negatively charged. These particles were found to be electrons. The observed current known as the photoelectric current is due to the flow of electrons.

After the study of photoelectric effect by Hallwachs, scientists J.J.Thomson, Lenard, Richardson, Compton did a series of experiments to study the relationship between photoelectric current, intensity of incident radiation, velocity and the kinetic energy of the photo electrons, and their dependence on the wave length of incident radiation used.

Effect of intensity of incident radiation on photo electric current

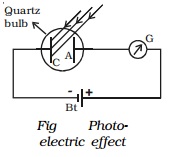
Keeping  the  frequency  of  the        Photo electric incident  radiation  and  the  potential          difference between the cathode and the anode at constant values, the intensity of       incident radiation is varied. The corresponding  photoelectric current is measured in the microammeter.    

It is found that the photo electric      current  increases  linearly  with  the intensity      of incident radiation (Fig).

Since the photoelectric current is directly proportional to the number of photoelectrons emitted per second, it implies that the number of photoelectrons emitted per second is proportional to the intensity of incident radiation.

Effect of potential difference on the photoelectric current

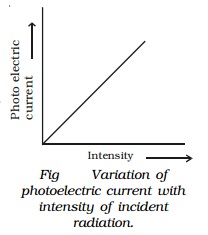
For a given metallic surface C, keeping the intensity (I₁) and frequency of the incident radiation constant, the effect of potential difference between the plates on the photoelectric current can be studied. Fig 7.3 shows the variation of photo electric current with the potential difference V between the two plates. When the positive potential of A is increased, the photoelectric current is also increased. However, if the positive potential is further increased such that it is large enough to collect all the photo electrons emitted from the plate C, the photoelectric current reaches a certain maximum value and this current is known as saturation current. If the potential of the plate A is made negative, the photocurrent does not immediately drop to zero but flows in the same direction as for positive potential. This shows that the photo electrons are emitted from the plate C with finite velocity. If the negative or retarding potential is further increased, the photo current decreases and finally becomes zero at a particular value. Thus, the minimum negative (retarding) potential given to the anode for which the photo electric current becomes zero is called the cut-off or stopping potential.

If m is the mass of the photo electron emitted with a velocity v_max then the kinetic energy associated with it is ½ mv²_max.

Since at the stopping potential V_o, the fastest electron is just prevented from reaching the plate A, workdone in bringing the fastest electron to rest = kinetic energy of the fastest electron. Since at the stopping potential V_o, the fastest electron is just prevented from reaching the plate A, workdone in bringing the fastest electron to rest = kinetic energy of the fastest electron.

eV_o = ½ mv²_max

The above equation indicates that the stopping potential depends upon the velocity of the fastest electron.

The experiment is repeated with the incident radiation of same frequency, but of higher intensities I₂ and I₃. It is found from the graph, the saturation currents are proportional to the intensities of the radiation. But, the stopping potential remains the same for all the intensities. Thus, for a given frequency of incident radiation, the stopping potential is independent of its intensity.

Effect of frequency of incident radiation on stopping potential

Keeping the photosensitive plate (C) and intensity of incident radiation a constant, the effect of frequency of the incident radiations on stopping potential is studied. Fig 7.4 shows the variation of the photo electric current with the applied potential difference V for three different frequencies. From the graph, it is found that higher the frequency of the incident radiation, higher is the value of stopping potential V_o. For frequencies ν₃ > ν₂ > ν ₁, the corresponding stopping potentials are in the same order (V_o )₃ > (V_o )₂ > (V_o )₁.

It is concluded from the graph that, the maximum kinetic energy of the photoelectrons varies linearly with the frequency of incident radiation but is independent of its intensity.

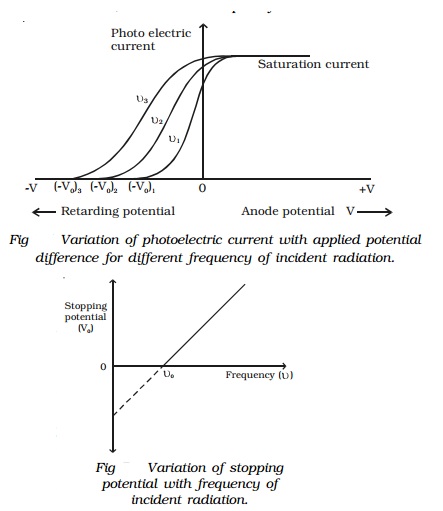
IIf the frequency of the incident radiation is plotted against the corresponding stopping potential, a straight line is obtained as shown in Fig 7.5. From this graph, it is found that at a frequency ν_o, the value of the stopping potential is zero. This frequency is known as the threshold frequency for the photo metal used. The photoelectric effect occurs above this frequency and ceases below it. Therefore, threshold frequency is defined as the minimum frequency of incident radiation below which the photoelectric emission is not possible completely, however high the intensity of incident radiation may be. The threshold frequency is different for different metals.

Laws of photoelectric emission

The experimental observations on photoelectric effect may be summarized as follows, which are known as the fundamental laws of photoelectric emission.

1.     For a given photo sensitive material, there is a minimum frequency called the threshold frequency, below which emission of photoelectrons stops completely, however great the intensity may be.

2.     For a given photosensitive material, the photo electric current is directly proportional to the intensity of the incident radiation, provided the frequency is greater than the threshold frequency.

3.     The photoelectric emission is an instantaneous process. i.e. there is no time lag between the incidence of radiation and the emission of photo electrons.

4.     The maximum kinetic energy of the photo electrons is directly proportional to the frequency of incident radiation, but is independent of its intensity.

Light waves and photons

The electromagnetic theory of light proposed by Maxwell could not explain photoelectric effect. But, Max Planck's quantum theory successfully explains photoelectric effect. According to Planck's quantum theory, light is emitted in the form of discrete packets of energy called 'quanta' or photon. The energy of each photon is E = hν, where h is Planck's constant.

Photon is neither a particle nor a wave. In the phenomena like interference, diffraction, polarisation, the photon behaves like a wave. In the phenomena like emission, absorption and interaction with matter (photo electric effect) photon behaves as a particle. Hence light photon has a dual nature.

Einstein's photoelectric equation

In 1905, Albert Einstein, successfully applied quantum theory of radiation to photoelectric effect.

According to Einstein, the emission of photo electron is the result of the interaction between a single photon of the incident radiation and an electron in the metal. When a photon of energy hν is incident on a metal surface, its energy is used up in two ways :

1.     A part of the energy of the photon is used in extracting the electron from the surface of metal, since the electrons in the metal are bound to the nucleus. This energy W spent in releasing the photo electron is known as photoelectric work function of the metal. The work function of a photo metal is defined as the minimum amount of energy required to liberate an electron from the metal surface.

2.     The remaining energy of the photon is used to impart kinetic energy to the liberated electron.

If m is the mass of an electron and v, its velocity then

Energy of the incident photon = Work function + Kinetic energy of the electron

hν = W + ½ mv²    …… (1)

If the electron does not lose energy by internal collisions, as it escapes from the metal, the entire energy (hν-W) will be exhibited as the kinetic energy of the electron. Thus, (hν-W) represents the maximum kinetic energy of the ejected photo electron. If v_max is the maximum velocity with which the photoelectron can be ejected, then

hν = W + ½ mv_max²    …… (1)

This equation is known as Einstein's photoelectric equation.

When the frequency (ν) of the incident radiation is equal to the threshold frequency (ν_o) of the metal surface, kinetic energy of the electron is zero. Then equation (2) becomes,

hν_o = W     …………………..(3)

Substituting the value of W in equation (2) we get,

hν - hν_o = ½ mv²_max

or

h(v-v₀)= ½ mv²_max

This is another form of Einstein's photoelectric equation.

Experimental verification of Einstein's photoelectric equation

Einstein's photoelectric equation is,

½ mv²_max = h(v-v₀)

½ mv²_max = eV₀

From equations (1) and (2)

eV₀ = h(v-v₀)

V₀= (h/e)v - (h/e)v₀     ………………………(3)

This is an equation of a straight line. Millikan verified equation (3) experimentally and found that it is in harmony with the observed facts.