Spectral series of hydrogen atom and Energy level diagram

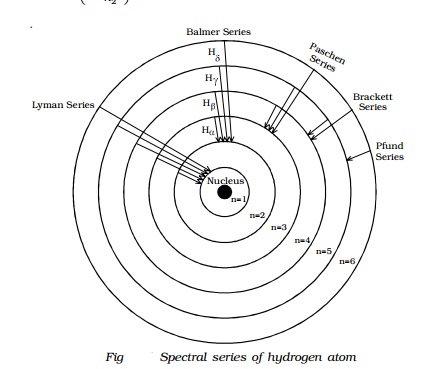
Spectral series of hydrogen atom

Whenever an electron in a hydrogen atom jumps from higher energy level to the lower energy level, the difference in energies of the two levels is emitted as a radiation of particular wavelength. It is called a spectral line. As the wavelength of the spectral line depends upon the two orbits (energy levels) between which the transition of electron takes place, various spectral lines are obtained. The different wavelengths constitute spectral series which are the characteristic of the atoms emitting them. The following are the spectral series of hydrogen atom.

(i) Lyman series

When the electron jumps from any of the outer orbits to the first orbit, the spectral lines emitted are in the ultraviolet region of the spectrum and they are said to form a series called Lyman series (Fig).

Here, n₁ = 1, n₂ = 2,3,4 …

The wave number of the Lyman series is given by,

v = R(1- (1/n²₂) )

(ii) Balmer series

When the electron jumps from any of the outer orbits to the second orbit, we get a spectral series called the Balmer series. All the lines of this series in hydrogen have their wavelength in the visible region. Here n₁=2, n₂ = 3,4,5 …

The wave number of the Balmer series is,

v = R( 1/2² - 1/n₂² ) = R( ¼  - 1/n₂² )

The first line in this series (n₂ = 3), is called the H_α-line, the second (n₂=4), the H_β-line and so on.

(iii) Paschen series

This series consists of all wavelengths which are emitted when the electron jumps from outer most orbits to the third orbit. Here n₂ = 4,5,6 … and n₁ = 3. This series is in the infrared region with the wave number given by

v = R( 1/3² - 1/n₂² ) = R( 1/9  - 1/n₂² )

(iv) Brackett series

The series obtained by the transition of the electron from n₂ = 5, 6... to n₁ = 4 is called Brackett series. The wavelengths of these lines are in the infrared region. The wave number is,

v = R( 1/4² - 1/n₂² ) = R( 1/16  - 1/n₂² )

(v) Pfund series

The lines of the series are obtained when the electron jumps from any state n₂ = 6, 7... to n₁=5. This series also lies in the infrared region. The wave number is,

v = R( 1/5² - 1/n₂² ) = R( 1/25  - 1/n₂² )

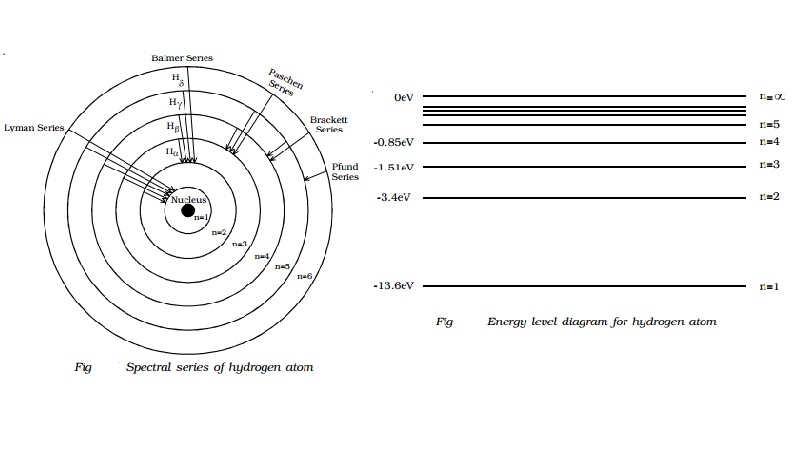
Energy level diagram

The energy of the electron in the n^th orbit of the hydrogen atom is given by,

En = -13.6 /n²   eV

Energy associated with the first orbit of the hydrogen atom is,

E₁ = -13.6 /1²   = -13.6  eV

It is called ground state energy of the hydrogen atom. Energy associated with the second orbit is given by,

E₂ = -13.6 /2²   = -3.4  eV

It is called energy of first excited state of the hydrogen atom. The energy of second, third, fourth, … excited states of the hydrogen atom are, E₃ = -1.51 eV, E₄ = -0.85 eV, E₅ = -0.54eV ...

when n =infinity ∞, E_inf = -13.6 / inf² = 0

Therefore, it is seen from the above values, that, the energy associated with a state becomes less negative and approaches closer and closer to the maximum value zero corresponding to n = ∞inf.

Taking these energies on a linear scale, horizontal lines are drawn which represent energy levels of the hydrogen atom (Fig). This diagram is known as energy level diagram.

Sodium and mercury spectra

The sodium vapour lamp is commonly used in the laboratory as a source of monochromatic (single colour) light. Sodium vapour lamps and mercury lamps have been used for street lighting, as the two lamps give a more intense light at comparatively low cost. The mercury light is a composite light consisting of all colours in the visible spectrum. The wavelength of prominent lines emitted by the mercury source is presented in Table 6.1. The two lamps work on the principle of hot cathode positive column. Since, sodium and mercury atoms are in the vapour state, they emit line spectra. The sodium vapour lamp emits yellow light of wavelength 5896Å and 5890Å. These lines are called sodium D₁ and D₂ lines.

List : Wavelength of spectral lines emitted by mercury

Colour   Wavelength (nm)

Violet     I        398

Violet     II       403

Blue                 436

Bluish Green I 492

Bluish Green II         496

Green              546

Yellow I 577

Yellow II         579

Orange   609

Red                  625