Determination of coefficient of viscosity of water by Poiseuille's flow method

Poiseuille's equation

Poiseuille investigated the steady flow of a liquid through a capillary tube. He derived an expression for the volume of the liquid flowing per second through the tube.

Consider a liquid of co-efficient of viscosity η flowing, steadily through a horizontal capillary tube of length l and radius r. If P is the pressure difference across the ends of the tube, then the volume V of the liquid flowing per second through the tube depends on η, r and the pressure gradient p/l.

(i.e) V α η^x r ^y (P /l)^z

V=k η^x r ^y (P /l)^z

where k is a constant of proportionality. Rewriting equation (1) in terms of dimensions,

[L³T^-1] = [ML^-1 T^-1] ^x [L]^y[ML^-1T^-2 / L]^z

Equating the powers of L, M and T on both sides we get x = -1, y = 4 and z = 1

Substituting in equation (1),

V= kPr⁴/ ηl

Experimentally k was found to be equal to π/ 8

V = πPr⁴ / 8 ηl

This is known as Poiseuille's equation.

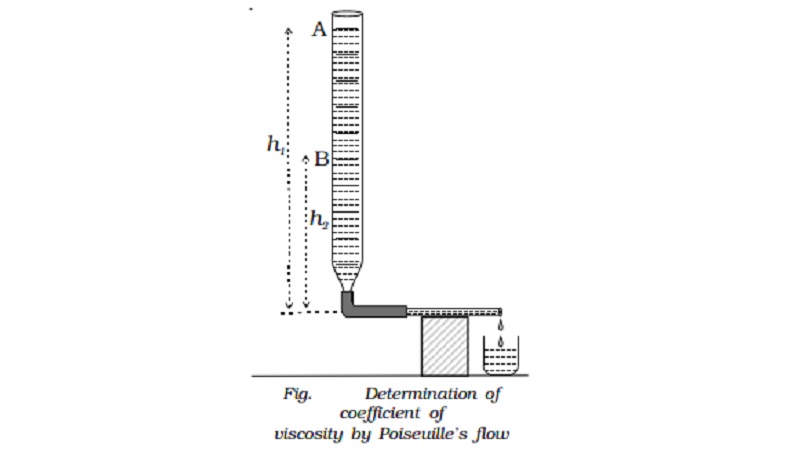
Determination of coefficient of viscosity of water by Poiseuille's flow method

A capillary tube of very fine bore is connected by means of a rubber tube to a burette kept vertically. The capillary tube is kept horizontal as shown in Fig.. The burette is filled with water and the pinch - stopper is removed. The time taken for water level to fall from A to B is noted. If V is the volume between the two levels A and B, then volume of liquid flowing per second is V/t. If l and r are the length and radius of the capillary tube respectively, then

V/t = πPr⁴ / 8 η

l

If ρ is the density of the liquid then the initial pressure difference between the ends of the tube is P₁ = h₁ρg and the final pressure difference P₂ = h₂ρg. Therefore the average pressure difference during the flow of water is P where

P = (P₁ + P₂ ) /2

=[(h1+h2) /2 ]hg

Substituting in equation (1), we get

V/t =  πhρgr⁴ / 8lη

or

η= πhρgr⁴t / 8lV

Viscosity - Practical applications

The importance of viscosity can be understood from the following examples.

(i)                   The knowledge of coefficient of viscosity of organic liquids is used to determine their molecular weights.

(ii)                The knowledge of coefficient of viscosity and its variation with temperature helps us to choose a suitable lubricant for specific machines. In light machinery thin oils (example, lubricant oil used in clocks) with low viscosity is used. In heavy machinery, highly viscous oils (example, grease) are used.